小圆平面靶磁控溅射镀膜均匀性研究

　　本文从圆平面靶磁控溅射的原理出发，针对圆形平面靶面积小于基片面积的特点进行分析，建立膜厚分布的数学模型，并利用计算机进行模拟计算，目的在于探寻平面靶材面积小于基片面积时影响膜厚均匀性的因素。模拟计算的结果表明：基片偏心自转时，靶基距和偏心距对膜厚分布均有影响。偏心距一定时，随着靶基距的增大，薄膜厚度变小，膜厚均匀性有提高的趋势；靶基距一定时，随着偏心距的增大，膜厚均匀性先变好后变差。当基片自转复合公转时，随着转速比的增大，膜厚均匀性逐渐变好，转速比增大到一定程度后，它对膜厚均匀性的影响逐渐变小。圆形平面靶的刻蚀环范围的变化对薄膜的均匀性有一定的影响。这些理论为小圆平面磁控溅射系统的设计和实际应用提供了理论依据。

　　为了在大面积基片上获得均匀性良好的膜层，人们做了很多研究。理论研究和实验证明，使用自转基片与溅射靶偏心布置可以有效增大膜层面积，采用基片自转加公转的复合运动形式有利于膜厚均匀性的提高。本文将针对这一情况，研究小圆平面靶在单独自转及自转复合公转时薄膜均匀性的变化规律，目的是为在较大基片上获得均匀的膜层提供理论基础。

1、膜厚分布模型

1.1、膜厚分布的物理模型

　　图1 为本文所研究的圆形平面磁控溅射系统示意图。如图所示，靶中心轴线与基片自转轴线的偏心距为e，垂直距离为H，靶上面元dA 距其轴线距离为r，基片上面元dB 距其轴线距离为R，dB 与dA 的中心距离为L，溅射角为β，面元dB 的法线与dA 的中心连线夹角为φ，面元dA的极角为θ。

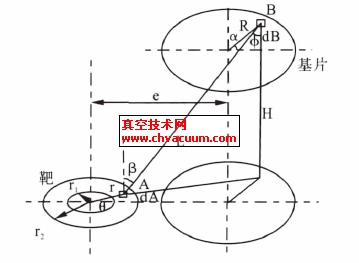
图1 平面磁控溅射示意图

　　为了计算溅射形成薄膜厚度的均匀性，对本论文所研究的平面磁控溅射系统可以作出如下假定^[1] ：

　　(1) 平面磁控靶磁极间区域为圆环状，该区域内横向磁感应强度最大，捕集于该区域内的二次电子使工作气体大量电离, 离子溅射主要发生于此。特假定：溅射出的粒子全部来自圆柱磁极到环状磁极圆环形区域内，在该区域内靶子受到均匀溅蚀，忽略圆环边缘电磁场畸变造成的影响。根据磁控溅射靶的刻蚀现象与磁控磁场的关系^[3] ，假设磁控溅射系统的溅射率与磁控磁场在靶表面的水平分量成正比。

　　(2) 入射离子集中在靠近靶面区域，在该区域内被电场加速使其能量提高，而导体靶表面电场处处垂直于导体表面，因而离子是垂直入射靶材表面的。故假定离子入射角为零。

　　(3) 认为被溅射的薄膜原子溅射到基片上后，无扩散运动，它们立刻停在原地不动，直接参与成膜，认为被溅射出来的薄膜原子离开靶表面的角度分布为简单的余弦分布，即用cos(β)表示，其中β 为出射角。

　　(4) 由于溅射过程必须充入工作气体，出粒子由靶至基片的空间飞行中被气体原子散射的现象不能忽略，但一般工作气压为零点几帕数量级，较为稀薄。故假定出射粒子由于空间飞行而被散射，其沉积在基片上的几率反比于路径长度L。

　　(5) 基片为圆形，圆形平面靶面与基片表面平行但中心不重合，偏心距为e。由图可知β=φ。这几条假定不会使推导结果产生很大的误差。

3、结论

　　基片自转时，在偏心距一定的情况下，随着靶基距的增大，薄膜厚度变小，膜厚均匀性有提高的趋势；靶基距一定时，随着偏心距的增大，膜厚均匀性先变好后变差。当基片自转复合公转时，随着转速比的增大，膜厚均匀性逐渐变好，转速比增大到一定程度后，它对膜厚均匀性的影响逐渐变小。在一定情况时，圆形平面靶的刻蚀环范围的变化对薄膜均匀性有一定的影响。相信这些理论将为小靶大基片磁控溅射系统的研究及应用提供一定的理论依据。

参考文献

　　[1] 孟宪权，任大志, 等. 环形磁控溅射成膜生长速率及厚度均匀性研究[J]. 武汉大学学报(自然科学版)，1995，41(3)：351- 356.
　　[2] 黄士勇，曲风钦，田晔，董维义. 用Monte Carlo 法模拟大型磁控溅射器的膜厚分布[J].真空电子技术，1999(5)：38- 42.
　　[3] Tatsuo F, Fumihiko S, Masahiko N. Observations on the Operation of a Planar Magnetron Sputtering System by Target Erosion Patterns [J].Thin Films, 1987, 151 (3):373- 381.
　　[4] 王小辉，卫红,等. 大面积户外照明光学薄膜膜厚均匀性研究[J].光学仪器，2006，28(4)：172- 175.
　　[5] 王晓冬，巴德纯，张世伟，张以忱.真空技术，冶金工业出版社，2006,9.