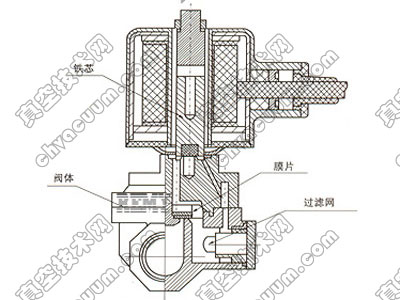
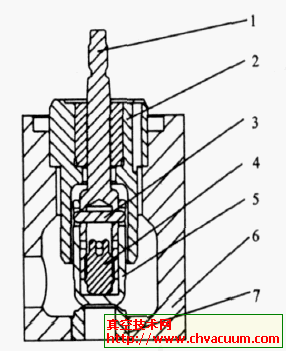
球面密封气动截止阀用气缸力的技术研究
1、概述
近年来随着加工工艺技术的发展,球面密封结构截止阀在航天试验系统中得到了广泛应用。航天氢氧火箭发动机试验系统(以下简称试验系统)有些部分处于低温或高压工作环境中,操作介质主要有液氧、液氮和液氢等低温介质及其他一些易燃有毒介质。所以试验系统中阀门的阀座一般采用不锈钢或铝合金等耐低温材料,而阀瓣一般采用F4、F46、聚酰亚胺或铜合金等材料。由于非金属密封材料在高压下工作时泄漏严重,所以试验系统中广泛应用了金属密封结构。本文以阀瓣为铜合金球形结构,阀座为不锈钢锥形结构的气动截止阀为例,介绍截止阀气缸力计算方法。
2、密封机理
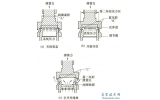
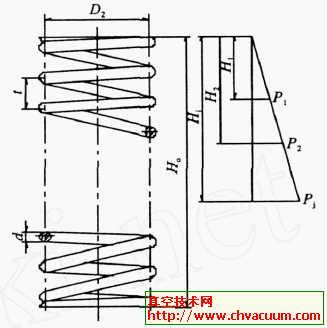
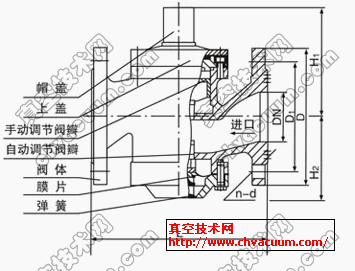
在截止阀中为保证流体的密封性,必须在密封表面间有一个相互作用的力(图1) ,即在密封表面上产生一定的比压,引起密封面微观不平度的变形,如果变形是在材料的弹性极限范围内,并造成不大的残余变形,那么接触面上的比压大于必须比压时,即可以保证其密封性。而在球面密封中,球面与锥面在气缸力作用下,根据接触表面的粘着理论,在简单载荷作用下真实接触点上的接触应力足以产生塑性变形,形成小的平面接触直到接触面承受全部载荷为止。由于铜合金球面的屈服强度比不锈钢阀座的屈服强度低,易于发生塑性变形。所以球面密封的形成过程就是球面和锥面之间相互接触发生弹塑性变形的过程,变形材料的塑性流动使接触面上的微观空隙逐渐填满,达到密封效果。
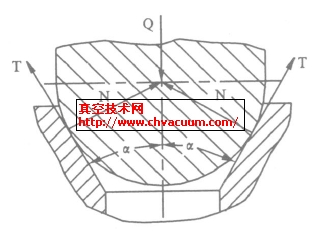
图1 锥形阀座结构和作用力
3、气缸设计
在气源压力一定时截止阀的气缸力主要与气缸内径有关,气缸内径主要与阀杆的受力有关。截止阀阀杆轴向受力有介质静压力QMJ、密封力QMF、摩擦力QT 和阀杆自重G等。对阀杆进行初期受力分析时,可以忽略摩擦力和自重的影响,待气缸内径确定后再复验气缸力是否能够克服摩擦力。介质静压力在阀门口径、压力和密封结构确定的条件下为已知力,密封力需要计算。在已有资料中,球面密封的线接触比压ql 只有在工作压力P ≤2.5M Pa的情况下才有准确的数据可以借鉴, 高于该压力的情况目前没有可以参考的数据。
3.1、传统设计方法
由于球体与平面接触时,在接触应力的作用下发生弹塑性变形,球体上会出现一个小的锥形带状密封面。假定密封宽度为b, 可以确定必须密封比压qM F和气缸直径。根据确定的气缸直径验算密封面的实际比压q是否大于必须密封比压qMF且小于许用比压〔q〕,气缸力是否能够克服阀杆摩擦力,如果不能满足要求,重新假定b值直到满足要求为止。举例,工作压力P=10MPa,阀门公称直径D=65mm,密封面直径DP=71.48mm,锥半角α=15°,气缸操纵气压力Pg=5MPa,球体材料为H62(屈服强度σsT=160MPa, 许用比压〔q)=80MPa ) , 阀体材料为0Cr18Ni9 (屈服强度σsG =205MPa) ,阀门气缸内径<115mm,介质从阀瓣下方流入。假定密封面宽度b=3mm,计算qMF、QMJ和QMF。
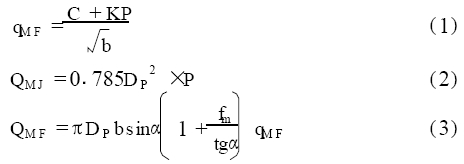
式中qM F ———密封面上的必需比压,M Pa
C———与密封面材料有关的系数(C = 3)
K———介质压力对比压值的影响系数(K = 1)
P ———工作压力( P = 10) ,M Pa
b———密封面宽度( b = 0.3) , cm
QM J ———介质静压力, N
Dp ———密封面中径(Dp=71.48) , mm
QM F ———密封面上密封力, N
α———锥半角, ( °)
fm ———密封面摩擦系数( fm = 0.2)
将数值带入式(1) 、(2) 和(3) 得到qMF=23.7MPa, QMJ=40109N, QMF=7213N。在忽略摩擦力的情况下得到阀杆轴向力QMZ=QMJ+QMF=47322N。阀杆轴向力即为气缸力F。
F = 0.785D2 P (4)
式中F ———气缸力, N
D ———气缸内径, mm
Pg ———气缸操纵气压力( Pg = 5) ,MPa
将数值代入式(4),得D=109mm。取D=115mm。依该直径对密封面比压进行校核,取摩擦力QT=3000N。