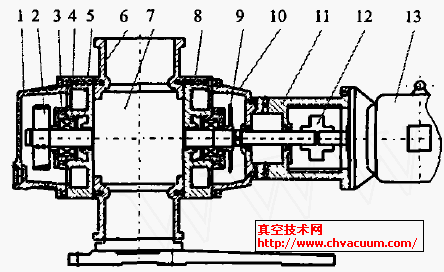
基于Pro/E的弧面分度凸轮参数化设计及有限元分析

　　以弧面分度凸轮工作轮廓面方程为基础，直接利用Pro E 中的曲线命令建立笛卡尔方程曲线，利用边界混合命令生成曲面，合并曲面，完成实体化特征。应用Pro/E集成的有限元模块Pro/MECHANICA进行结构的有限元分析，得到静态分析、失稳分析、模态分析受力云图，为改进设计提供了参考依据。模型的一致性好、数据完整，克服了专业有限元分析软件前处理不足的缺点，提高了有限元分析的工作效率。

　　引言

　　弧面分度凸轮机构在动力学性能、承载能力、分度的精度以及分度的速度方面均有不可比拟的优越性。采用Pro /E5. 0 软件对弧面分度凸轮特征进行参数化建模，以参数化模型的特征建立相应系列化关联点，生成系列化产品模型。并对弧面分度凸轮进行结构分析，找出应力薄弱处，为提高零件设计强度提供参考，确保产品设计的合理性，减少设计成本，缩短设计周期。Pro/Engineer Wildfire5. 0 软件是PTC 公司基于单一数据库、参数化、特征、全相关及工程数据再利用等概念开发出的一个功能强大的CAD/CAE /CAM 软件。Pro/Engineer 的最大特点就是基于特征的参数化建模，参数化模型以约束来表达产品模型的形状特征，以一组参数来控制设计结果，从而通过变换一组参数值方便地创建一系列相似零件。其自带的Pro/MECHANICA structure 是集静态、动态结构分析于一体的有限元模块，能够模拟真实环境为模型施加约束及载荷，进行静态分析、失稳分析、模态分析等。与现有主流有限元分析软件前处理功能相比，建模能力优势明显，模型的一致性好、数据完整，从而可以提高设计工作效率。

1、弧面分度凸轮三维建模

　　1.1、弧面分度凸轮计算公式

　　弧面分度凸轮工作轮廓面方程:

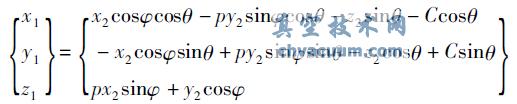
　　弧面分度凸轮通用共轭接触方程:

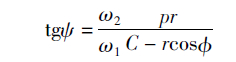
　　上面两式中，p —凸轮分度期廓线的旋向符号，左旋p= + 1，右旋p = - 1; ω1—凸轮的角速度; ω2—从动盘的角速度; C—凸轮与转盘间的中心距; —从动盘上滚子的位置角，是滚子的起始位置角与滚子的角位移之和; r、ψ 为从动盘上滚子圆柱形工作面方程式中的曲面参数。

4、结束语

　　以弧面分度凸轮工作轮廓面方程为基础，直接利用Pro/E 中的曲线命令建立笛卡尔坐标方程的分度期曲线，利用偏移命令和镜像命令建立间歇期的曲线，再将生成的曲线合并成曲面，完成实体化特征。与现有的编程法及二次开发相比，无需专业的编程背景，该方法简单易操作。利用Pro/Engineer Wildfire5. 0 集成的有限元模块Pro/MECHANICA 环境中进行结构分析，借助静力分析、模态分析、失稳分析等结构分析的受力云图，发现廓面设计缺陷，为结构改进提供了依据。