U形波纹管膨胀节刚度和应力计算(2)
1.2、膨胀节整体弹性刚度计算
(1)轴向刚度
(a)单式膨胀节整体刚度Kx=fi/N (7)
(b)复式膨胀节整体刚度Kx=fi/2N (8)
(2)侧向刚度
(a)单式膨胀节整体刚度Ky=(1.5Dm2fi)/[LbN(Lb±X)2] (9)
(b)复式膨胀节整体刚度Ky=(KuDm2fi)/[4NLu(Lu-Lb±X/2)] (10)侧向刚度计算中,轴向位移X拉伸时取“+”,压缩时取“-”。
(3)整体弯曲刚度
Kθ=(πDm2fi)/(1.44×106N) (11)
2 未加强U形波纹管的应力计算
(1)内压引起的周向薄膜应力σ2
由图39可知,当受内压P作用时,在一个U形波的纵截面上的内力与作用在半个环壳上的外力平衡。
4(πr+α)δmσ2=qDmP
σ2=(qDmP)/[4(πr+α)δm] MPa (12)
几何尺寸r、α有如下关系:
r=q/4
α=h-q/2 (13)
将(13)式代入(12)式,得周向薄膜应力为:
σ2=(DmP)/[2mδm(0.571+2h/q)] MPa (14)
(2)内压引起的径向薄膜应力σ3
当波纹管受内压P作用时,在以D与Db为直径的两个环形截面上的内力与轴向外力平衡,则:
π(D+Db)δmσ3=(π/4)(D2-Db2)P (15)
因D=Db+2h,代入上式,经整理后得:
σ3=Ph/2δmm MPa (16)
(3)内压引起的径向弯曲应力σ4
在经线为半个U形环壳上切出单位宽度的窄条(见图40),设两端固定,并受均布压力P作用,可得最大弯距为:
M=P·h2/12 (17)
断面系数为:W=πDmδm2/6 (18)
则径向弯曲应力为:
σ4=M/w=P·h2/2δm2 MPa (19)
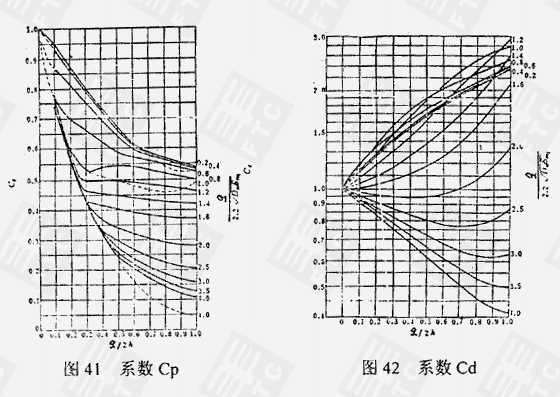
考虑形状尺寸的影响,引进修正系数(EJMA法)得:
σ4=(P·h2Cp)/2cm (20)
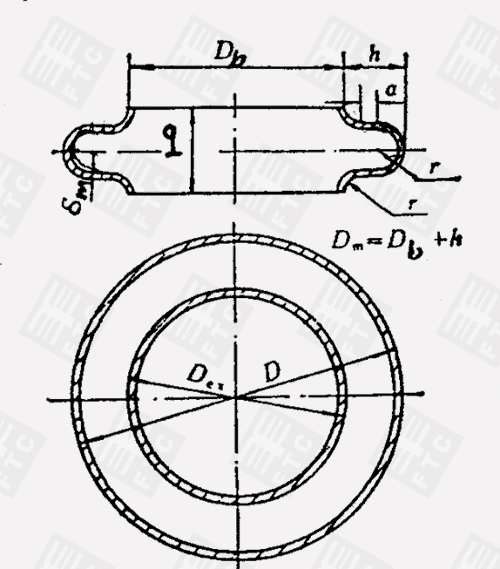
图39 U形膨胀节的几何参数。

图40 环壳上的几何尺寸
(4)由轴向力Fex引起的径向薄膜应力σ5
由式(3)、式(4)可得:
σ5=Fex/πDmδm=(1.7Eδm2ex)/(πh3Cf) MPa (21)
按EJMA法修正后,其公式形式为:
σ5=(Eδm2ex)/(2πh3Cf) MPa (22)
式(22)为实际计算公式。
(5)由轴向力Fex引起的径向弯曲应力σ6
可以证明在Fex作用下,最大弯矩发生在波顶B处(见图37),其值为:
Mmax=Fexh/2 (23)
断面系数为:W=πDmδm2/6 (24)
则弯曲应力为:σ6=Mmax/w=3Fexh/πDmδm2 MPa (25)
引入公式(3)、(4)的关系,得:σ6=(5Eδmex)/(πh2Cd) MPa (26)
按EJMA法修正后得:
σ6=(5Eδmex)/(3h2Cd) MPa (27)
(6)应力评定
a、薄膜应力
σ2≤Cwb[σ]bt (28)
σ3≤[σ]b
b、弯曲应力:σ3+σ4≤Cm[σ]bt (29)
c、经向总应力范围:
σt=0.7(σ3+ σ4)+σ5+σ6 (30)
以上介绍的U形膨胀节计算的方法,尽管由于力学模型的简化,给计算结果带来一定程度的误差,但因公式比较简单,又根据实际情况进行了修正与调整,故在工程设计时仍然得到广泛的应用。
U形膨胀节也可看作环壳与环板的组合体,承受轴对称的载荷。列出平衡方程进行求解也可得出计算公式。但其过于繁复,不便于应用。
近年来利用有限元法对膨胀节的应力分析研究工作也取得了进展。它以有限单元的集合代替无限单元的连续体,作物理上的近似,通过能量原理得出离散方程,经过求解,可以得到各离散单元的应力与位移的数值解。有利于进行精确的设计计算。