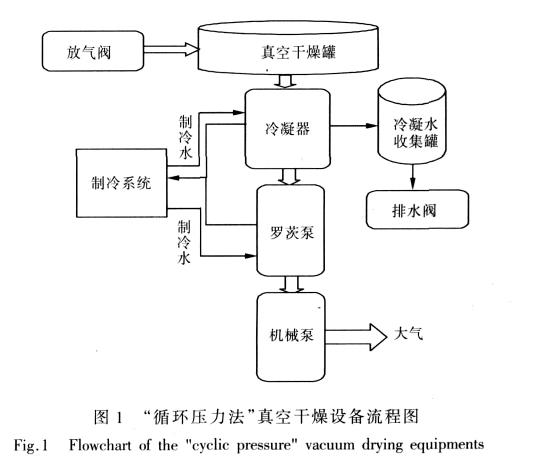
液体真空制冷的理论分析及实验验证
本文建立了真空制冷的数学模型,对绝热和有热交换情况下的真空制冷过程进行了理论分析,推导了两种情况下液体温度随时间的变化函数;讨论了影响液体温度变化的各种参数,其中系统压强ps 、液体初始温度Tf0、汽液交界面面积A和外界热源Q 是影响液体温度变化的主要因素。在理论计算基础上,进行了实验验证,并对二者进行了分析比较。实验数据和理论计算结果非常吻合,理论计算能够很好地预测水温的变化趋势。
真空制冷的基本原理是利用抽真空降压而使液体相变蒸发而制冷。在真空制冷的过程中,当外界压强降低到液体所对应的汽化压强时,液体就汽化相变,从而带走大量的蒸发潜热。当系统与外界绝热时,沸腾所带走的蒸发潜热来自于液体自身的能量,使其冷却下来,达到制冷降温的目的。
目前真空制冷的研究主要集中在食品冷冻工业,文献[1]综述了真空制冷在食品工业中的各种应用,文献[2]建立了真空冷却的非稳态数学模型,并利用CFD软件对多孔食品的真空冷却进行了数值模拟。文献[3]综述了真空冷却技术在花卉、果蔬和熟肉中的应用研究现状以及目前真空冷却技术理论研究的进展。真空制冷具有冷却速率快、冷却均匀、蒸发潜热大等优点,随着微电子芯片功率不断增大,真空制冷有望成为冷却微电子芯片的一种新技术。
世界上第一个液体真空制冷模型由Burfoot[4]提出,他认为在气相和液相之间存在一个浓度梯度,并假设蒸发水的质量流量和质量传递系数与水蒸汽的平衡压力和系统总压力的压力差成正比例。Hous-ka[5]、Zitny[6]分别提出了二个不同的真空制冷模型。这些模型是基于气相和液相的热力学平衡而得到的。Petera 和Dostal[7]等对液体真空制冷的基本原理、数值模拟作了研究,并对Houska 的模型和Zitny的模型作了比较。
尽管Dostal[8]提出的真空制冷模型很好地分析了真空制冷中的传热现象,但仅停留在绝热条件下,且没有对推导的结论作实验验证。本文在Dostal工作的基础上,建立了真空制冷系统热传递的数学模型,分别在绝热和有热交换条件下对真空制冷系统中的液体温度的变化进行了分析,推导两种情况下液体温度随时间的变化函数,分析影响温度的各种参数并对理论模型进行实验验证,从而为利用真空制冷冷却微电子芯片提供理论依据。
1、液体真空制冷的数学模型
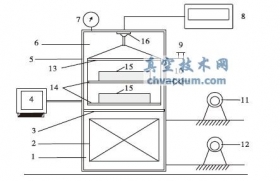
真空制冷系统的物理模型如图1 所示,为了简化计算,作如下假设[8]:
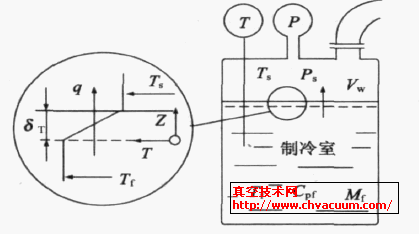
图1 真空制冷系统的物理模型图
(1) 在气相和液相之间存在热力学平衡,并认为该平衡处于液体表面和其蒸汽之间。
(2) 由于在汽液表面间进行的传热传质过程存在着一定的阻力,在靠近气液界面的一个薄层内,存在着明显的热传递阻力和质量传递阻力。
(3) 汽液交界面的温度Ts由饱和蒸汽压Ps所对应的平衡值来确定,在液体内部温度处处相等。
(4) 在制冷过程中, 整个系统真空度保持恒定;在液体表面上方空间只有饱和水蒸汽而没有其它气体。
由图1 所示,热传递发生在汽液界面的液体薄层内,从等温液体流向气液界面的热流量qz, 写成一维形式可表示为
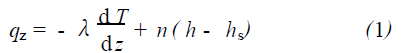
式(1) 中T 是液体的温度,λ是液体的导热系数, n 是对流质量通量, h 、hs分别是液体内部和气液界面(移动面) 上的比焓。而焓可以表示为热容cpf与温度的积。于是式(1) 可改写为:
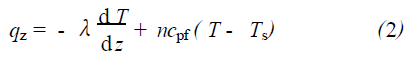
式中T、Ts 分别为液体内部温度和气液界面(移动面) 的平衡温度。
对式(2) 在z 轴方向作积分, 边界条件为z = 0时, T = Tf , z =δT 时, T = Ts ,则式(2) 转化为:
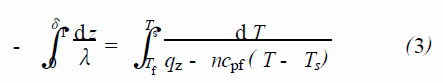
忽略在积分区间内参数的变化,热流量qz 可以表示为:
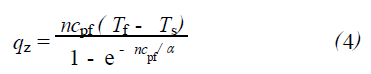
上式中α是汽液界面薄膜换热系数,是由液体薄膜的热阻δT/λ= 1/α确定的。
在式(1) 和(2) 中, 为了确定液体对流质量通量n ,假设在液体中, 对流质量传递是主要的传质过程,分子扩散可忽略。因而质量通量n 可以表示为质量传递系数kc 和浓度差Δρf 的乘积。由于蒸发作用,蒸汽的密度远小于液体的密度,因此我们可以把汽液交界面上的质量通量n 表示为kcρf , 代入到式(4) ,得到:
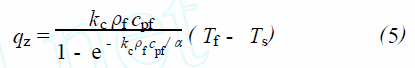
式(5)确定了通过气液交界面的热流量。从液体中带走的总的热流量可以用qz 和气液交界面面积A的乘积来表示。下面将分两种条件分别推导液体温度随时间变化的关系式:
(1) 若系统与外界绝热,则在汽液交界面下方的控制体积内,液体的非稳态热平衡可表示为:
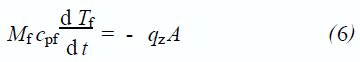
假设在制冷过程中, 部分液体蒸发并从液体中带走蒸发潜热。由于蒸发的液体质量远小于固定控制体积内的质量, 因此假设在短时间内Mf 是一个常数。
其中Mf ( kg) 为初始质量(包括水和容器的质量) , A为汽液界面面积,将式(5)代入式(6)并积分,考虑液体初始温度为T f0 , 得到随时间变化的液体的温度Tf :
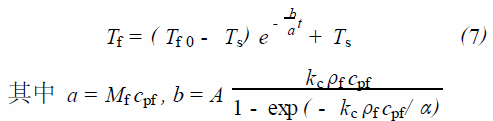
(2) 若系统与外界有热交换,恒定的热源功率为Q,则在汽液交界面下方的控制体积内,液体的非稳态热平衡可表示为:
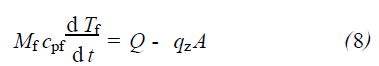
将式(5) 代入到式(8) 并积分, 考虑液体的初始温度为T f0 ,得到随时间变化的液体的温度Tf :
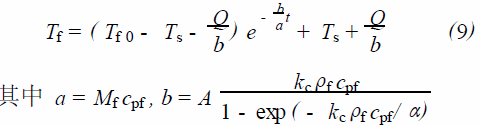
从式(7)和(9)可以看到,液体的温度Tf 与液体初始温度T f0 、液体饱和温度Ts、液体初始质量Mf 、汽液界面面积及液体的热物性参数有关。液体饱和温度Ts 与真空系统中所能达到的最低饱和蒸汽压ps 有关, 正如假设(3)所述, 汽液交界面的温度Ts由ps 所对应的平衡值来确定,即Ts 和ps 是一一对应的, 它们之间的关系由热力学决定。ps 越小, Ts也越小, 则Tf 也越低; 汽液界面面积A 越大, 汽化速率越快,则液体的温度Tf 越低;而在有热交换的条件下,液体的温度Tf 不仅与上述参数有关, 还与外界的换热量Q有关, Q越大,则Tf反而越高。