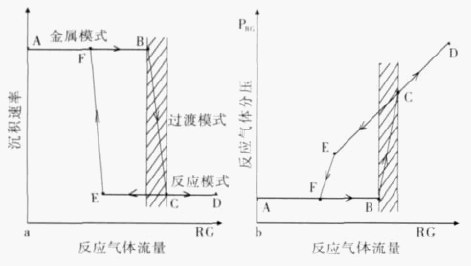
冲击载荷作用下金属薄膜缺陷的多尺度分析

2014-10-27 姜文全东北大学机械工程及自动化学院

　　应用多尺度方法研究金属薄膜-基体结构中的缺陷在冲击载荷条件下的变化规律和力学行为。多尺度方法结合了分子动力学和有限元方法，分子动力学方法用于纳米薄膜中的局部缺陷区域，有限元方法用于整个膜-基结构，微/宏观尺度之间的握手区通过FEAt 方法进行连接。模拟计算既包括了系统宏观尺度上的模型位移、应力场等，又包括了微观尺度上原子位置坐标、缺陷附近原子结构变化等。模拟结果表明: 在冲击载荷作用下，冲击波通过基体传递到薄膜；在宏观上，体现为膜-基结构应力的变化；在微观上，缺陷附近原子发生溅射。可见由于冲击作用产生的应力集中和缺陷处原子溅射导致膜-基结构中的微缺陷进一步扩大，造成薄膜失效。

　　随着镀膜工艺的发展，金属薄膜的厚度已由数微米发展到数纳米的超薄膜，它兼具传统复合材料和现代纳米材料二者的优越性。纳米薄膜可以改善一些机械零部件的表面性能，以减少振动，降低噪声，减小摩擦，延长寿命。但此类金属薄膜在制备过程中，经常会产生一些微裂纹，真空技术网(http://www.chvacuum.com/)认为这使得薄膜的力学性能受到极大的影响。近年来，在单一尺度下的金属薄膜上的微裂纹研究，已引起了研究人员的一定关注；但对于多尺度下的金属薄膜缺陷鲜有研究。为此，文中应用多尺度方法对带有表面缺陷的膜-基结构进行模拟研究，旨在多角度地揭示金属薄膜失效机理。

1、多尺度仿真基本原理

　　对于多尺度问题，在原子区及连续介质区的计算方法都已相对成熟，主要难题集中在如何处理原子模型和连续介质的握手区上，文中采用FEAt 方法对握手区进行仿真。在FEAt 方法中，整个模型划分成1、2、3、4 四个部分，如图1 所示。

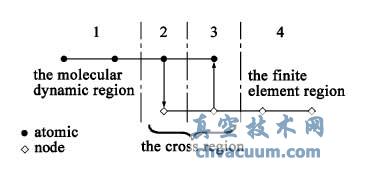
多尺度区域划分

图1 多尺度区域划分

2、多尺度模拟计算

　　2.1、多尺度模型建立

　　在不锈钢基体上镀100 nm 厚铜膜，膜-基结构材料常数见表1，薄膜表面带有宽10 nm，深50 nm表面微裂纹。建立多尺度模型如图2 所示: 整个模型分为有限元区( 基体部分) 、握手区( 薄膜和基体结合部分) 、分子动力学区( 薄膜部分) 。细划握手区有限单元体长度，实现节点与原子一一对应，即有限单元体的长度等于原子晶格常数。

表1 膜-基结构材料常数

冲击载荷作用下金属薄膜缺陷的多尺度分析

图2 多尺度模型

　　2.2、模拟计算过程

　　对基体左右两端施加UY 约束，底面加载10 kN外力冲击，作用时间为1.0 × 10 ^-8 s；有限元模拟与分子动力学模拟时间步长比为1∶ 1000；在握手区，有限元模拟计算求得位移增量加权平均，其值代入到应用FEAt 方法自编程序中，求得分子动力学边界条件( 即边界原子以1000 m/s 向薄膜内部冲击) 。