真空管道流导计算中平均压力取值的误差分析与计算方法
真空管道的流导,又叫做通导能力。它是管道的重要性能参数,是设计真空系统时必须考虑的因素之一。在计算粘滞流管道流导时,流导跟管道内的平均压力有关,通常的方法是近似把管道入口压力作为管道平均压力。但是当管道较长、真空泵抽速较低或管道入口压力较小时,上述近似方法的误差就变大了。本文对粘滞流下管道的平均压力的取值进行了讨论,分析了近似取管道高压端压力为平均压力时所产生的误差,并提供了粘滞流下管道的平均压力的计算方法等。
1、目前真空管道粘滞流态流导计算中的问题
在粘滞流态下的管道流导与真空管道内的平均压力p 有关。通常管道的平均压力取为:

式中:p1 为抽气管道的进口压力,p2 为抽气管道的出口压力,即真空泵的入口压力。在真空系统设计中,通常仅是知道真空室内的压力,即抽气管道入口处的压力,因此在计算抽气管道的平均压力时,一般都是近似把抽气管道入口处的压力作为管道的平均压力。其理论根据是,在真空系统抽气过程中,仅是在粗抽阶段存在粘滞流,而粗抽管路的流导C 一般都比较大。根据真空技术基本方程,在泵的抽速Sp 较低、管道流导C 较大的情况下,真空泵对真空室的有效抽速Se 近似等于真空泵在入口压力下的抽速Sp, 即若C垌Sp时, 则Se≈Sp。则根据气体连续性方程可得:Q=p1Se=p2Se,所以p1≈p2,从而得到p=p1。但是,这仅是在假设粗抽泵的抽速相对于抽气管道的流导来说很小时,这样的近似取值方法才存在一定的合理性。但是在粘滞流下管道的流导与平均压力成正比,随着真空泵的不断抽气,管道的流导逐渐下降,当泵的抽速与管道的流导相差不大时,就会存在较大的偏差。下面我们对平均压力近似取值为抽气管道入口端压力时的误差进行定性地分析。当管道为长管时,把式(1)代入流导定义式可得粘滞流圆截面管道流导为
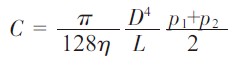
假设真空泵的抽速Sp 不变,则Q=P2Sp,根据管道流导的定义得
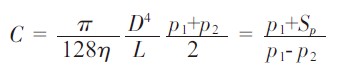
解得:

注意,上面两式中Sp 实际上是对应泵入口压力p2 下的抽速,在Sp 未知的情况下,仅在抽速Sp 为常数的压力范围内有解。当抽速随着真空泵入口压力变化时,因Sp 是随着p2 变化的,而p2 未知,所以无法确定抽速Sp,从而无法计算管道的平均压力。
2、真空管道平均压力的误差分析与计算方法
由上所述,在真空管道粘滞流态的流导计算中,当真空泵的抽速发生变化时,需要对真空泵的抽速曲线进行数值化拟合,建立p2 与Sp 之间的函数关系,从而可以根据p2 与Sp 之间的关系和上述公式进行联立方程组解算出管道出口压力p2,即可计算出管道的平均压力p,从而进一步准确计算管道的流导。
例如,假设真空泵连接真空室的管道D=0.04 m,L=1 m,真空泵的抽速为8 L/s,气体为20℃的空气。若管道入口处压力,假设真空泵抽速S 不变,此时由于L/D>20,管道为长管,则由式(2)得:

若近似把抽气管道入口压力近似取为管道的平均压力,即p=p1=100 Pa。从以上计算可以知道,在这个算例中,当系统压力(管道入口压力)较高时,这两种管道平均压力确定方法的取值偏差很小,相对误差仅约为1.2%。但是当管道入口压力较低时,两者取值偏差就会很大。例如,真空系统条件同前(D=0.04 m,L=1 m,S=8 L/s),使用该泵从大气压抽到10 Pa时,其平均压力的取值相对误差随着管道入口压力的变化曲线如图1 所示,由图可以看出,若是管道入口压力很高时,此时管道的流导也很大,管道的平均压力p 近似取入口压力p1,相对误差很小,随着入口压力的降低,管道的流导也降低,相对误差也会增大,此时近似把管道入口压力取值为平均压力就不适用了。由图可以看出,随着管道入口压力的下降,相对误差逐渐增大,最大相对误差达到了11.5%。
对于短管道:当D=0.04 m,L=0.5 m,S=8 L/s时,使用同一台真空泵从大气压抽到10Pa 时,由于L/D>20,管道为短管,假设真空泵抽速为常数,使用式(3)计算p2,其相对误差随着导管入口压力的变化曲线如图2 所示。误差趋势和长管时的误差趋势一样,最大误差达到了5.7 %。由图1 和图2 可以看出,即使当真空泵抽速为常数,在管道直径一定的情况下,当管道的长度变化时,其最大误差亦发生较大的变化。
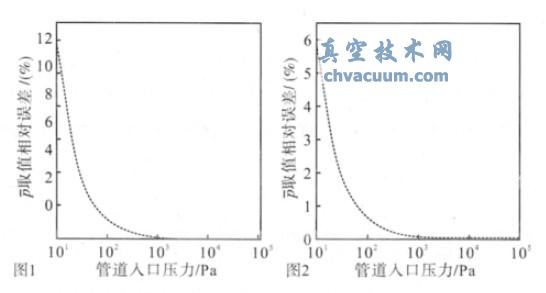
图1 相对误差随着管道入口压力的变化曲线(长管)
图2 相对误差随着入口压力的变化曲线(短管)
当D=0.04 m,S=8 L/s 时,近似把管道入口压力取值为平均压力时,其相对误差随着管道入口压力、管道长度的变化如图3 所示。从图可以看出,随着管道长度的变化,其最大误差也逐渐增大,当L=5 m 时,最大相对误差达到了45%。所以,若是管道太长,近似取值法是不适用的。这主要是因为管道长度越长,管道的流导就越小,管道进口和出口的压差变大,若是再使用近似取值法,相对误差也会随着管道长度增大而增大。

图3 相对误差随着入口压力和管道长度的变化
当D=0.04 m,L=1 m 时,近似把管道入口压力取值为平均压力时,其相对误差随着入口压力、泵的抽速(在每一抽速下,视为常数)的变化如图4 所示。从图可以看出,随着真空泵的抽速的变化,其最大误差也逐渐增大,当S = 100 L/s 时,误差达到了70%。所以,若是泵的抽速太大,近似取值法是不适用的。
综上所述,在计算粘滞流态下真空管道的流导时,当管道较短、泵的抽速较低、入口压力较高时,管道平均压力近似取值的相对误差较小,反之,相对误差较大。所以在计算粘滞流态管道的流导时,应该根据具体情况分析是否可以近似取抽气管道入口处压力为平均压力。
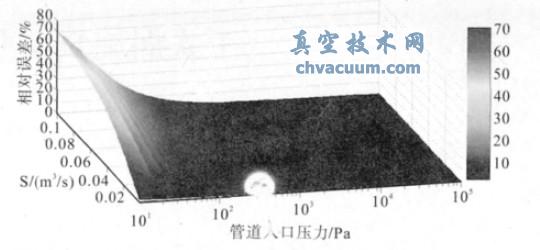
图4 相对误差随着入口压力和泵抽速的变化
在流导计算过程中,可以根据真空泵的抽速曲线数值化后的数组来假定在对应压力范围内真空泵的抽速为常数,然后采用式(2)、式(3)计算出管道出口处的压力p2,根据式(1)计算出管道的平均压力p,再计算粘滞流态下管道的流导,从而减少计算粘滞流态下管道流导的误差。