������糣�����״�Ŀ��ɢ������Ӱ��
��������Ŀ����״�ɢ����������Ŀ��Ĵ�С����״������ǵ��й����Ŀ��ĵ�������йأ�������Եĺ��ľ��ǽ�������Խ�糣����Ƶ�ʵı仯����Ƶ����½�糣���Ǹ�������Ų��ڵ�����������Ӧ���������ɢ�䳡��ͬ�ߴ�ǽ���Ŀ����״�ɢ�����ҪԶС�ڽ���Ŀ���״�ɢ����棻��Ƶ����£���糣����Ϊʵ�������������ǵ�����ǵ�����ˣ��������Ե��һ����������Ų���ͬ�ߴ�ķǽ���Ŀ��ļ����״�ɢ��������ֵ���Դ��ڽ���Ŀ��ļ����״�ɢ����档
����
���������о����������������ͬһ�ߴ硢ͬһ���ϵĽ���ƽ��ͽ��������״�ɢ��������ֵ���кܴ����ġ����״�ɢ�����( RCS) һ���������Ų���Ƶ����ֱ�ӹ�����������λ�ں���ļ����״�ɢ�����( LRCS) ͨ���������Ų���Ƶ��û��ֱ�ӹ������������ڱ���ֲڳ̶ȡ�������Ⲩ�����ڵ�Ų��������ֶ��ǽ�����ͳһ���״﷽�����Ƶ����״�ɢ�����ı���ʽ����ͬһĿ����������뼤���״�ɢ�����ȷ����ֺܴ�IJ��죬���ֲ������Խ�������Խ�糣��Ƶ�ʱ仯�����ԣ��ڴӵ�Ƶ����Ƶ�Ĺ����н�糣����ʱ��Ϊʵ������ʱ��Ϊ��������ʱ��Ϊ������ʱ��Ϊ����������Щ���ԶԲ�ͬƵ���½���Ŀ����״�ɢ�����Ĵ�С��������ҪӰ�졣
2����ͬƵ���µĽ�����糣��
������������ʵIJ����Ҫ�ǵ����ڲ���һ���ֵ�����“���ɵ�”������������һ��ԭ���У������������Ӿ�����“����”�˶���ʵ����”���ɵ���”������ȫ���ɣ���Ϊ�����ܵ����ӵ����ã����յ綯��ѧ�е�ų�����ʵ�����õ��й����ۣ����ƺ��˶��ĵ�����Ϊһ����г����������ģ�ͣ�ÿ�����ӱ��ָ����������ţ����ܵ�Ψ���������������Ϳɵý����е������ⳡ�����µ��˶�����Ϊ��
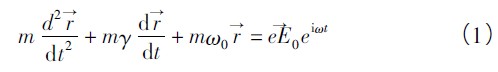
����ʽ�У�ω0Ϊ���ӵĹ�������Ƶ�ʣ�m Ϊ����������ωΪ�ⳡ��Ƶ�ʣ�γ Ϊ����ϵ����
������������г����������ģ�͵��˶����̵Ľ⼰�����еĵ���λ�Ƽ������й�֪ʶ�������˽�������Խ�糣���ı���ʽ��

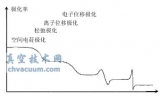
����ʽ�У��趨ÿ��ԭ������f0�����������ɵģ������ⲿ�ֶԽ�糣�������������ʽ��γ0�����ɵ������ⳡ�����µ�����ϵ�����й�������ʾγ0≈1013 Hz ���ҡ���һ���������ͨ������£�εr���ⳡƵ��ω�ĺ���������һ�����������Ƕ�ʽ( 2) �����о����Եó�����:�������Ų�Ƶ�ʱȽϵ͵������( ω��γ0) ��һ��ȡω < 1011 Hz���Ϳ�����Ϊ“��Ƶ”�����������ߵ粨��������ʱ��������Խ�糣����һ����������������Խ�糣�����ܴ��������Ե�Ų��������ڽ����в��ϲ��������ȣ�����ʱ��Ե���е���Խ�糣��Ϊʵ�����������Ե�����ܴ��������Ų�Ƶ����1013 < ω < 1015 Hz ��Χʱ�������⡢�ɼ��⣬��ʱ��Խ�糣����һ��������������n ��һ����������������µ�Ų���������������ڲ�����Ų�����ȫ�������������ȥ��������ʾ�����Ӱ㷴�����ԣ���Ϊ��������������ʱ���������Ե��û�б������𣻵�Ƶ�ʸ��ߵ������( ω >1015 Hz) �������⡢X ���ߣ���Խ�糣����һ��������������n ��һ��ʵ������ʱ�������е�����������ԣ�����������“��”��һ�����Ų����������������ȡ�
3��ͬһ��������Ŀ�꼤���״������״ﲻͬɢ���������۽���
�����״�ɢ�������һ�����Ա���Ŀ��ػ�ز�����������������������Ŀ��ʶ��Ŀ������о�����Ҫ���á����ۼ����״ﻹ�����״����̫�����״��ɢ�������Ƶ��������״﷽�̣����״�ɢ�����Ķ���Ҳ����ͬ�ġ�
���������״�ɢ��������ض��壬�������״����ƽ��ͽ���������״�ɢ�����( RCS) ���Էֱ����Ϊ��
�������ۿ���֤��������ֱ����ʱ���ΪA�Ľ���ƽ���RCS��

����ʽ�У�A Ϊƽ��������λ Ϊ���IJ�����σ ��ka /λ2�ı仯������ͼ1 ��ʾ��
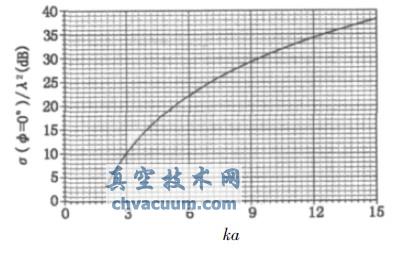
ͼ1 ����ƽ��ķ������RCS ��ka �ı仯��ϵ
4������
����(1) ���������״�ɢ�����Ĵ�С������Ӳ�Դ������йػ�������λ�йأ���ɢ�䲨֮������ɵģ����ڹ�ѧ��������Ϊ����ʣ��������Ե��һ����������Ų�����ʱɢ���֮�䲻����ɵģ��״�ɢ�����Ĵ�С��ֻ����Ӳ�Դ������йء�������״�ɢ������벨���йأ��������״�ɢ������벨�������ء�
����(2) �����״�ɢ������ǰ��պ������ѧ�ķ�����������ģ�Ŀ�����ֲڵ�״����Ӱ�켤���״�ɢ��������������أ�ͬ�ߴ�ķǽ����ɲ���ļ����״�ɢ��������ֵ���Դ���ͬ�ߴ���ɰ��������ļ����״�ɢ����棻����Ƶ����µ����״�ɢ������ǰ��յ�Ų������۽�������ģ���Ҫ���ݵ������˹Τ���̣���Ų��ڵ������������Ӧ��������Щ��Ӧ�ĵ�����������ɢ�䳡���Ӷ���RCS �������ף����ڷǽ����ڲ����������Ӧ������Ҳ�Ͳ��ἤ��ɢ�䳡������ڵ�Ƶ�����ͬ�ߴ�ǽ�������״�ɢ�����ҪԶС�ڽ������״�ɢ����档
����(3) �����ڸ�Ƶ���ǵ�Ƶ����½���������״�ɢ�����Ĺ������������֡�һ�ǵ����ڸ�Ӧ��������ɢ�䳡���״�ɢ�����Ĺ��ף����ǵ���ֲڱ����ɢ����״�ɢ�����Ĺ��ף��ڸ�Ƶ����£�����ֲڵ�Ӱ������Ҫ�ģ�����Ų��ڵ�����������Ӧ�������Ժ��ԣ��ڵ�Ƶʱ��Ų��ڵ������������Ӧ����������ɢ�䳡�Ƕ�RCS ����Ҫ���ף�������ֲڱ����ɢ������ֻ��һ���ţ����Ժ��Բ��ƣ���������������ν�ʲ�����ȫ���Ա����ɾ��塣
����(4) �״��ɢ����������Ŀ��Ĵ�С����״�����䲨�IJ���������ǵ��й����Ŀ��ĵ�������йأ�������Եĺ��ľ��ǽ�������Խ�糣����Ƶ�ʵı仯�����ֳ���ȫ��ͬ�����ԣ��ڵ�Ƶ��Ӱ��Ŀ���״�ɢ������С����Ҫ������Ŀ��ĵ�����Ժ����䲨�IJ��������ڸ�Ƶ���ڣ����״�ɢ����������Ϊ����������ɢ��ĵ��ӣ�������������״��ϸ��Ӱ��ϴ�
����(5 ) ̫���ȵ�Ƶ��λ���������֮��( 1012 Hz) ����һ���ν����Ľ�糣������ӵĹ������������ԣ���̫�����״�ɢ�����Ȳ���ͬ����Ҳ����ͬ�ں��⣬����ӵĹ�����Ҫ��һ��̽����ʵ����