基于有限元分析的粉末介电常数测试装置研制
针对固体粉末的特点,研制了一种测试其介电常数的装置。设计了电容传感器,采用有限元方法对其进行仿真,得出了传感器的电场矢量图,分析了传感器的等效电路;以AD7746芯片为核心,搭建了电容测试电路及电容输入范围扩展电路;采用屏蔽线、屏蔽罩提高测试系统的稳定性及精度。装置所能测试的电容值达到fF量级,应用所设计装置测试了不同密度下二氧化硅粉末的相对介电常数,实验结果表明:本装置能够稳定、准确地测试固体粉末的相对介电常数。
1、引言
相对介电常数是电介质或绝缘材料物理特性的一个重要参数,许多理论及工程应用研究,特别是以电容传感器为核心的检测技术,例如电容层析成像技术、粉末混合物均匀度测试、物质含量检测等诸多研究均建立在各种物质的不同介电常数基础之上。因此,对物质介电常数的精确测定对了解物质性能以及开发相关测试设备具有举足轻重的作用。
根据测试对象的不同,研究人员设计出了各种类型的物质介电常数测试仪器。HEERENS设计了一种带有保护环的电容测试装置,其保护环接地,在两块平板中间产生均匀的静电场,进而可以精确测得两平板间的电容;朱兆青设计了一种基于USB的介电常数测试仪,该仪器能够实现对固体及气体介质的介电常数的测试;江畑克史公布了一种可用于测量由粉末和液体介质组成的混合物质的相对介电常数的方法及设备。针对固体粉末难以成型的特点,本文设计了一种可用于测试固体粉末介电常数的装置,该装置主要包括双圆筒式电容传感器、电容测量电路,同时文中还提出了一些提高测试精度的方法。
2、电容传感器设计
由基尔霍夫电容公式,计及边缘效应的两圆形平行极板间的电容值可近似地表示为:
式中:εr为极板间物质的相对介电常数;εo为真空中的介电常数,其值为:8.854×10-12 [F/m];r为圆极板半径[m];d为两极板之间的距离[m]。
由式(1)可以看出,两圆形平行极板间的电容值由2部分组成,前一项表示由均匀场产生的电容值,后一项表示由边缘效应附加的电容,若忽略此项,当两极板间的距离d及极板的半径r确定时,通过测定两极板间的电容值就可以得出极板间物质的相对介电常数。然而,在实际测量中,由于边缘效应形成的附加电容相当大且随着参数的变化而变化,这必然会严重影响测试结果的精度,增加测试的复杂性。另外,由于固体粉末难以成型,因此在测量时必须有一容器装盛被测物料。结合以上几点,本文所设计的电容传感器结构如图1所示。该传感器总体尺寸为40×20(mm),主要包括上、下极板,内、外圆柱筒以及保护环和衬板,其中待测粉末放在内圆柱筒中,其尺寸为25.3×17.1(mm)。上、下极板、保护环的材料是紫铜,其余零件均采用聚四氟乙烯加工而成,聚四氟乙烯具有良好的机械加工性能,故能保证传感器设计所要求的平行度、同轴度等要求。
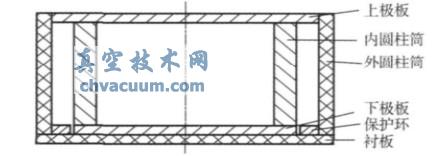
图1 电容传感器结构
由于固体粉末之间存在间隙,故内圆柱筒中的物质应为空气与固体粉末的混合物,因此本系统测得的是两极板间该混合物的电容值。
为进一步研究此传感器的电场特性,本文用ANSYS软件建立了其有限元模型,建立过程主要步骤如下:
1)建立模型,本文建立的传感器轴对称模型如图2所示;
2)设置单元属性;本模型的单元类型为PLANE121;空气的相对介电常数设置为1,聚四氟乙烯的相对介电常数设置为2;
3)采用三角形网格划分相应面;
4)设置边界条件并加载,本模型中上极板上加载的电压为5V,下极板及保护环上的电压均设置为0V;
5)求解。

图2 电容传感器有限元模型
结论
本文提出了一种固体粉末介电常数测试装置,设计了电容传感器、电容测量电路,采取了提高测试装置稳定性的措施。随着固体粉末在化工、航天、医药、食品、塑料制品等行业越来越广泛的应用,必然需要更多、更精确的以工艺过程控制、产品混合均匀度测试、物料含量检测等为目的的仪器,以期优化产品的过程控制、提高产品质量,本研究能够为此类仪器、设备提供必要的理论支持及基础数据,具有重要的适用价值及广阔的应用前景。