活塞式压力计的基本原理及应用(3)
计算实例:
下面是气体活塞压力计的一个例子,它的物理参数,包括砝码值,由厂家提供。
示例:
在Ta= 20 ℃,Pr=6.9MPa时,计算需要施加的砝码质量。
设备:
气体活塞压力计主机:RUSKA2465-754
活塞系统:RUSKA2465-729
专用砝码组: RUSKA 2465-799
环境:
g1 - 978.72346 cm/sec2
P(ref) - 大气
ρa - 0.00118 gm/cm3
h-0 cm (无高度差)
根据式(10)可计算所需的砝码质量M a(表观值),也可用下式计算:
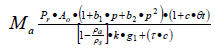 (11)
(11)
已知参数分别为:
Ao = 8.39086E-02 cm2 ( 20oC)
b1 = 3.0E-06 m2/m2/MPa
b2 = 0.0
c = 9.1E-06 m2/m2/oC
ρa = 0.00118gm/cm3
k = 1/980.665 cm/sec2
g1 = 978.72346 cm/sec2
θt = Ta -20 = 20-20 = 0oC
ρs = 8.0 gm/cm3
Pref = 大气
p = 标称压力
Pr = 6.9 MPa / 9.80665 = 70.3604187kg/cm2
(1+b1.p) = (1+ 3E-06.70.36) =1.000211081
(1+c·θt) = 1+0.0000091 . 0 = 1
k · g1 = 978.72346/980.665 = 0.99802018
(1 - ρa/ρs) = 0.9998525
代入式(11),可计算得到需要的砝码质量为:
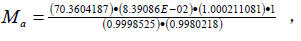
即:
Ma = 5.917677488 a M kg
由此,可以得到需要施加的砝码的质量:
M total= Ma- tare mass (kg) (12)
上式中,tare mass 是活塞及连接件的质量。
M total = 5.917677483-0.01178538 = 5.905892103
从砝码组中选取合适的砝码,并利用克组、毫克组砝码进行精确调整,施加需要的砝码质量,具体过程为:
M total= 5.905892103-0.5000266 1# 砝码=5.40586550-1.0000569 2# 砝码= 4.40580860-1.0000866 3# 砝码= 3.40572200-1.0000839 4# 砝码= 2.40563810-1.0000300 5# 砝码= 1.40560810-0.9999244 6# 砝码= 0.40568370-0.2999771 8# 砝码= 0.10570660-0.10000382 10# 砝码= 0.00570278kg即 5.703 grams 克、毫克砝码
在活塞上按以上顺序加上砝码,调整活塞系统压力使其处于厂家标记的工作位置(参考平面)后,就可以确认:压力计产生的压力就是计算出的压力值。
在该示例中,活塞压力计产生的压力与大气压有关,活塞的参考面,包括砝码,都置于当地的大气环境中,工作在表压测量模式;如果参考压力减小到绝对零压,那么活塞产生的压力就是绝对压力。为实现绝压工作模式,通常用一个钟形的玻璃罩将质量块封装在其内,用排量合适的真空泵, 将玻璃罩内的气体抽出。
但将玻璃容器抽成高真空是很难实现的,应测量出内部的残余压力,并列入压力的计算式中。这样得到绝对的压力—力值关系式如下:
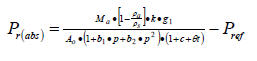 (13)
(13)
上式中不包括表面张力修正项,是因为绝压通常只用气体活塞压力计产生,基本上不用考虑气体介质表面张力的影响。
高度差修正
前文叙述的压力—力值关系式考虑,即式(10),仅在活塞压力计的参考平面上是成立的,实际应用中,我们往往更关注被测试设备的受压点的压力。这需要对系统内流体(气体或液体)的高度差造成的压力差进行补偿。进行表压模式测试时,参考压力(气压)随高度的变化也必须考虑。
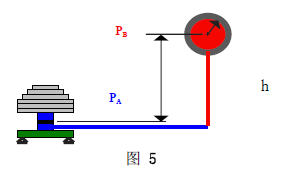
以图5为例,活塞参考平面处的压力以PA表示,被测仪表感压点的压力以PB 表示,则:
PB=PA-(k·g1·ρf·h+k·g1·ρa·h) (14)
式中:
k = 比例系数
h = 被测试仪表感压点与活塞参考平面的垂直高度差。被测试仪表在活塞参考面上方时为正,下方为负
g1 = 当地重力加速度
ρf = 流体介质密度,随压力改变而变化,在介质为气体时尤为明显。
ρa = 空气密度。通常取 0.00118g/cm3, 也可根据使用地点的气压、温度、相对湿度计算得到。
通过以上修正,可得到被测仪表处的压力为:
PB=PA-k·g1·h(ρf-ρa) (15)
上述修正看起来似乎意义不大,其实不然。看下面的例子:若活塞压力计所用工作介质(油)的密度为0.9 gm/ cm3,则每厘米液柱产生的压力约为0.0009 kgf/cm2。当活塞压力计工作压力为100 kg/cm2,液柱高度差为1厘米时,如果不对高度差进行修正,将产生9ppm 的测量误差(0.0009%);如果高度差为10cm,则测量误差可达到90ppm(0.009%);在这个高度差下,如果活塞压力计工作压力为10kgf/cm2,则由液柱高度差引起得的误差可达到900ppm(0.09%)。
结论
许多文献对活塞压力计的原理进行了很好的论述,但关于活塞压力计实际应用中需要考虑的因素的论述却少之又少。以上经验的获得来之不易,希望能对活塞压力计用户有所裨益。
研制活塞压力计的最终目的是产生或测量出准确的压力。
压力测量的误差来源主要有三方面,分别是:标准仪器、被校验仪器本身,以及使用人员和使用环境。要对测量结果的不确定进行分析,必须对以上三个方面的因素进行全面考虑。
“准确度”是通过压力基(标)准装置的检定确定的,通常由有能力的权威计量部门给出。通过计量部门的量值传递,可以给出活塞压力计的技术特性(有效面积、压力系数、质量等),并给出以上参数的测量不确定度。
活塞压力计的技术性能也必须明确,包括:重复性、灵敏度、稳定性,温度系数等。这些由仪器制造商提供。操作人员和环境所产生的误差也必须进行客观的分析、量化或控制。活塞压力计没有固有的“准确度”,它仅仅是一个工具,它的工作特性(随机的和系统的)应包含在压力计量的全过程中。