单座式调节阀阀芯-阀杆系统流固耦合振动研究
针对单座式调节阀阀芯-阀杆系统的流固耦合振动问题,建立了考虑阀门定位器作用的系统动态仿真模型,给出了求解阀芯-阀杆系统响应的预估-校正算法,利用ANSYS软件对系统在固定开度与变开度情况和流开型与流闭型情况下的振动响应进行了定性分析。研究表明:对于固定开度,阀芯稳态位移偏移量以及流体力随压差增加以及开度减小而增大,阀芯动态位移过渡时间随压差增加而缩短,而流开型流向时阀芯位移响应幅度要大于流闭型流向。对于开度减小情况,采用流闭型流向时阀芯动态位移过渡时间更短,且压差越大,阀芯动态位移过渡时间越短,而流开型流向时则相反;对于开度增大情况,阀芯动态位移过渡时间和压差之间的关系与开度减小情况相反。
调节阀在水利、电站、化工、石油、冶金等过程控制系统中起着重要作用,然而调节阀在某些工况下产生的振动往往成为引起各种事故的主要原因,振动严重时甚至影响系统安全平稳地运行。导致调节阀振动的主要原因是阀体内部流体流动的不稳定性,与流固耦合作用直接相关。
流固耦合导致的调节阀振动可以分为两种:一种是调节阀整体在管道上的振动;另一种是本文要研究的调节阀自身阀芯-阀杆系统振动。国内外有关阀流固耦合振动的研究较少,且大多偏重于在某些固定开度、单一流向工况下分析阀体及流道内的瞬态流场及其与阀体或阀芯、阀杆的弹性振动之间的流固耦合相互作用,例如分别对调节阀、电磁阀、截止阀、换向阀以及溢流阀等不同类型的阀的动态特性与流固耦合问题进行了仿真和试验研究。
本文以某型号单座式调节阀为对象,研究调节阀阀芯-阀杆系统在流开式与流闭式流向、固定开度与变开度工况时的流固耦合振动问题。通过建立考虑定位器作用的系统有限元流固耦合模型并进行仿真,分析流开型和流闭型调节阀阀芯-阀杆系统在固定开度和变开度条件下的动态响应。
1、阀芯-阀杆系统动力学模型
1.1、单座式调节阀结构
单座式调节阀整体结构如图1所示,主要由执行机构和调节机构组成。执行机构将控制器输出电流信号转换为调节阀阀杆的直线位移;调节机构通过阀杆与执行机构相连,并将位移信号转换为阀芯和阀座之间流通面积的变化,从而改变流经阀体的流体运动状态。为了使阀芯和阀座之间的开度稳定在某个特定位置以保证实现控制器所要求的目标状态,调节阀设有阀门定位器附件,组成以阀杆实际位移为测量信号、以控制器电流输出为设定信号的反馈控制系统。
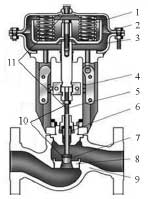
图1 单座式调节阀结构示意图
1.弹簧2.膜片3.气室4.位移刻度5.阀杆6.填料7.阀芯8.阀座9.阀体10.调节机构11.执行机构1.2 阀芯-阀杆系统动力学模型
阀芯-阀杆系统是调节阀执行-调节机构的主体,主要包括薄膜膜片、推杆、弹簧、填料、阀杆、阀芯和阀座等,如图1所示。
对于特定调节阀结构,其调节性能主要取决于阀芯-阀杆相对阀座的运动。阀芯-阀杆与气室弹簧、填料、流体等组成一个流固耦合动力学系统。在建立阀芯-阀杆动力学模型之前作如下假设:调节阀内部的流体(水)是不可压缩的;在调节阀工作过程中,水没有热交换;阀杆与填料之间的摩擦力认为是一种粘性阻尼力;整个阀体为刚性体,忽略其弹性变形;阀芯-阀杆只沿轴线运动,不考虑横向运动;单座阀的执行机构为气动正作用执行机构。
根据以上假设以及单座阀的结构图,可以将阀芯-阀杆系统简化为一个单自由度质量-弹簧-阻尼系统,如图2所示。阀芯位移坐标原点设在阀门全关的位置,取向上为正方向。
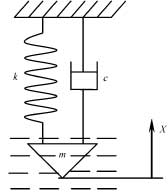
图2 阀芯-阀杆系统动力学模型
根据图2所示,单座阀阀芯-阀杆系统动力学方程为
———阀芯t时刻的位移、速度及加速度
m———阀芯-阀杆系统的总质量
k———弹簧刚度系数
c———等效粘性阻尼系数
Fc(t)———执行机构作用在阀芯上的控制力
Fl(t)———流体不平衡力
g———重力加速度
式(1)中流体不平衡力Fl(t)(以下简称流体力)是指行程调节机构中流体作用在阀芯上的轴向合力,其大小与调节阀两端的压差、阀芯大小和形状、调节阀类型、阀上游压力、流体流向及流体物理特性等因素有关。对于流开式流向(图1中流体从左侧流入,右侧流出),流体力为
式中 p1———阀前压力 p2———阀后压力
Δp———前后压差 ds———阀芯直径
dz———阀杆直径
对于流闭式流向(图1中流体从右侧流入,左侧流出),流体力为
对于动态问题,无论流开式还是流闭式流向,阀芯受到的实际流体力Fl(t)由阀芯上下分布的压力(通过预估-校正有限元流固耦合计算)对阀芯表面面积积分求得。为了使求解过程简化,可以将流体力近似认为流体压力在阀芯等效横截面积上作用的结果。
式(1)中控制力Fc(t)是指执行机构作用在调节机构阀芯-阀杆系统上的轴向力,其大小与电-气阀门定位器结构参数、控制器输出电流信号产生的电磁力以及阀芯位移有关。阀门定位器是调节阀的主要附件。它将阀杆位移信号作为输入的反馈测量信号,以控制器输出信号作为设定信号,将二者进行比较,当两者有偏差时,改变其到执行机构的输出信号,使执行机构动作,从而建立了阀杆位移信号与控制器输出信号之间的一一对应关系,即
式中 p、q、T———与定位器结构性能有关的参数
N(X0)———与指定目标位移X0成比例的电磁力
因此,调节阀阀芯-阀杆系统动力学方程可写为
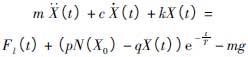 (5)
(5)2、阀芯-阀杆系统流固耦合问题求解
由于前面建立的调节阀阀芯-阀杆系统动力学方程中的流体力Fl(t)无法用准确的解析表达式表示出来,需要通过有限元流固耦合方法计算得到。本文采用ANSYS12.0中的CFD模块对调节阀内部流场进行分析计算,首先建立内部流场的几何模型,然后对不同工况下的调节阀流场进行计算,求得流体力。调节阀内部流场几何模型可以通过三维建模软件SolidWorks来建立,计算流场时需要对ANSYS中的CFD模块的流固耦合方法进行改进。
2.1、流固耦合分析典型步骤
通过ANSYS软件物理环境方法对阀芯-阀杆系统进行流固耦合分析。阀芯-阀杆会在流体力作用下发生位移,位移的大小将改变阀芯移动壁面边界,从而显著影响流场的形状。流固耦合分析通过在结构分析中得到阀芯移动壁面位移,用于流场分析。具体流固耦合分析的典型步骤如下:
(1)创建整个几何模型:包括流体区域和调节阀阀体结构区域。
(2)创建流体物理环境:给流体区域赋予单元类型,还要确定迭代次数,激活湍流模型,施加边界条件。
(3)创建结构物理环境:清除在流体物理环境中设定的信息,准备定义结构物理环境。转换单元类型并设定单元选项,将流体区域单元设定为NULL,将结构区域赋予单元类型,施加结构边界条件,定义合适的载荷步和求解选项,然后写入结构物理环境文件。
(4)流体/结构求解循环:在本系统中,入口的速度作为总体收敛的准则。当两次Flotran求解的入口速度差值足够小时,求解结束。初始Flotran分析设置的迭代次数应当多一些,以利于较好地收敛。随后的流体分析由于是在前一次流体分析基础上重启动,因此,迭代次数可以少一些。结构分析同样也需要重启动。对于非线性分析,节点必须在重启动以前恢复到初始位置。本文计算一共执行了5次耦合迭代,第1次Flotran分析共迭代100次,以得到较高的收敛精度,随后的4次Flotran分析各迭代40次,即可满足精度要求。一共迭代260次,取前250次数据即前0.25s的位移响应。
2.2、阀芯-阀杆系统流固耦合模型预估-校正求解算法
由于调节阀阀芯与流场接触面为移动壁面,ANSYS软件的典型流固耦合方法难以满足计算要求,本文采用预估-校正算法[8]来解决这种情况下的流固耦合问题。根据阀芯-阀杆系统动力学方程(5)和预估-校正算法,可得出阀芯-阀杆系统的预测步和校正步计算表达式,分别为
预测步
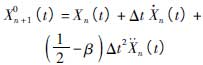 (6)
(6)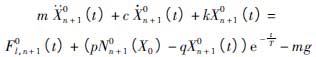 (8)
(8)第r步校正步
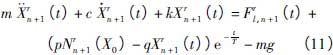
2.3、阀芯-阀杆系统流固耦合有限元模型建立
2.3.1、调节阀内部流场几何模型创建
调节阀的内部流场就是调节阀内部充满流体后所占的空间。假设阀体、阀芯是刚体,流场的边界是阀体、阀芯与流体的耦合面,阀体与流体之间的耦合面是不动的,而阀芯与流体之间的耦合面是移动的(包括固定开度下的振动和变开度时的移动)。由于假设阀芯是刚体,所以在做流场分析时,需要将阀芯部分挖去,对于不同的开度,只需要将对应阀芯位移的不同位置挖去即可,由于阀杆对流场的影响比较小,所以在建立的模型中忽略阀杆。调节阀的内部流场模型如图3所示。

图3 调节阀内部流场模型
2.3.2、网格划分
本文采用自由网格划分方法。在划分网格之前首先要设置单元类型,并为实体模型分配单元属性,本文中的流场模型采用的是Fluid142单元。阀芯与流体之间的耦合面流场变化比较大,采用最大为0.002的网格划分,而其他部位阀体与流体之间的耦合面,采用最大为0.004的网格划分,根据划分结果,共有单元102306个,节点20531个。网格划分结果如图4所示。

图4 流场模型网格划分
2.3.3、载荷施加
在网格划分之后,要对模型施加载荷以及边界条件,本文中对模型施加的具体条件如下:
(1)入口:定义压力为0.2~2.1MPa。
(2)出口:定义压力为0.1MPa。
(3)固定壁面条件:所有与阀体接触的耦合面上流体流动速度为零,相对位移为零,即除了进出口端面和阀芯周围的耦合面外,其余边界上速度和位移均为零。
(4)移动壁面条件:与阀芯接触的耦合面上的流体速度和位移应该与阀芯的运动速度和位移一致,即当阀芯静止时,耦合面上的流体速度和位移均为零;当阀芯运动时,耦合面上每个节点的任何时刻的速度和位移大小都与阀芯上对应节点的速度和位移大小相同。由于本文只考虑阀芯轴向运动,所以以上提到的位移和速度均指轴向位移和轴向速度,其余方向的位移和速度都为零。
(5)不考虑温度变化,即不涉及热交换。
3、阀芯-阀杆系统流固耦合动态响应分析
通过求解阀芯-阀杆系统流固耦合模型,仿真计算调节阀在不同边界条件下阀芯受到的动态流体力以及阀芯-阀杆系统的动态位移响应,分析定位器对调节阀阀芯振动的影响,考察阀内介质流向不同时,阀芯在固定开度和变开度的振动情况,找出阀芯受到的动态力与位移、压差之间的关系。
3.1、阀门定位器对阀芯-阀杆系统动态响应的影响
假设阀芯在目标位移15mm处,分别在进出口压差为0.1、0.5、1.0、2.0MPa下工作,介质流向为流开状态,初始相对位移为-0.1mm,初始速度和加速度均为零,初始流体力为50N。分别对比分析带有阀门定位器和没有阀门定位器时阀芯-阀杆系统的阀芯位移和流体力响应,如图5、6所示。
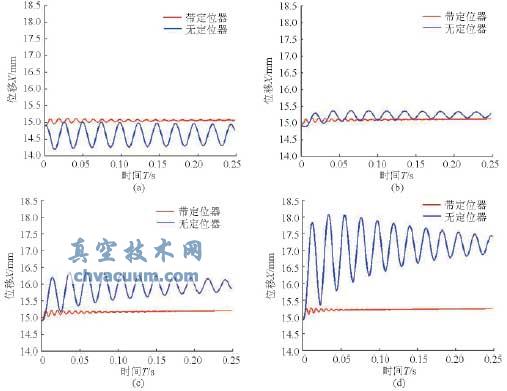
图5 单座阀阀芯的振动响应对比
(a)压差0.1MPa(b)压差0.5MPa(c)压差1.0MPa(d)压差2.0MPa
由图5可得:带有定位器比无定位器时阀芯振动波动小得多,而且趋近目标平衡位置的时间更短。在较大压差(0.5~2.0MPa)下,无论是否带有定位器,压差越大,阀芯振动偏离目标位置越远,并且振幅越大,而带有定位器的调节阀工作状态更为稳定、精确。
由图6可以看出:随着压差增大,无定位器的阀芯受到的流体力波动也随之增大,而带有定位器的阀芯受到的流体力变化则一直保持平稳,并且逐渐从小于前者的均值过渡到大于其均值。
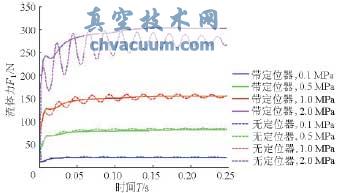
图6 单座阀阀芯受到的流体力对比
3.2、单座阀在固定开度下的动态特性分析
假设调节阀阀门全关位置为坐标原点,取向上为正方向,总行程为0(全关位置)~25mm(全开位置),进出口压差变化范围为0.1~2.0MPa,介质流向分别为流开和流闭。考察阀芯在目标位移(指定开度)作自由振动时阀芯的振动情况。
3.2.1、不同流向对单座阀动态特性的影响
在某个目标位移下,阀芯在受到初始运动条件的扰动时,会在平衡位置作自由振动。假设阀芯分别在不同目标位移(3、5、10、15、20、25mm)下和不同进出口压差(0.1、0.5、1.0、2.0MPa)下工作,初始相对位移为-0.1mm,初始速度和加速度均为0,不同工况下初始流体力不同,考虑定位器作用,得出介质流向不同时单座阀阀芯的位移与阀芯受到的流体力随时间变化历程。图7为某固定开度(目标位移为10mm)时阀芯位移与阀芯所受流体力的时间响应历程。图8为位移、压差与流体力的三维关系图和二维关系图(为便于比较,图中流闭时的流体力均取正值表示)。
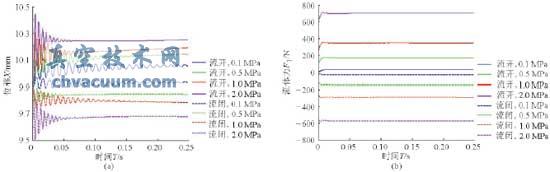
图7 固定开度不同压差下的振动响应
(a)位移响应(b)流体力响应
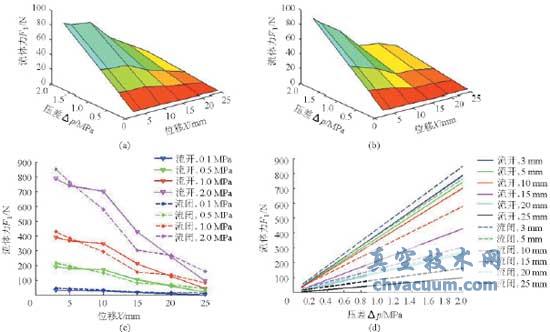
图8 动态流体力与位移、压差之间的关系
(a)流开状态三维表示(b)流闭状态三维表示(c)位移为参数(d)压差为参数
由图8可以看出:
(1)在不同的目标位移下,无论介质流向为流开或者流闭,流体力总是随压差增大而线性增长。
(2)在不同的进出口压差下,无论介质流向为流开或者流闭,流体力随着位移的增大(开度增大)而减小。
(3)在较小压差(0.1MPa)下,流开状态下的流体力总是小于流闭状态下的流体力;在较大压差(0.5~2.0MPa)下,在阀门接近全开和全关位置时,流开状态下的流体力小于流闭状态下的流体力,而阀门在中间位置时,流开状态下的流体力大于流闭状态下的流体力。
3.2.2、不同流向对阀芯位移偏移量的影响
阀芯在不同压差下趋向目标开度的过程中,实际工作开度相对设置目标开度对应的阀芯位移之间有一定的偏移量。根据不同压差、位移下阀芯运动仿真,可以得到不同介质流向时阀芯偏移量与压差、位移之间的关系,如图9所示(为便于比较,图中流闭时的偏移量均取正值表示)。
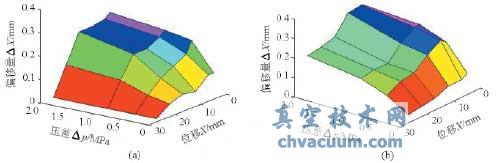
图9 偏移量与压差、位移之间的关系
(a)流开状态(b)流闭状态
由图9可以看出:
(1)在较小压差(0.1MPa)下,流开状态下阀芯偏移量要比流闭状态下的偏移量大;在较大压差(0.5~2.0MPa)下,流闭状态下的偏移量总体要比流开状态下的偏移量大;且各种工况下的偏移量都在允许的范围(3%~5%)内,能够满足定位精度。
(2)在同一个目标位置处,压差越大,偏移量越大。
(3)在同一压差下,目标位移越大,偏移量越小。
3.3、单座阀在变开度下的动态特性分析
阀芯在受到流体力和控制力作用时,会从初始位置向目标位置运动,并最终保持在目标位置附近作振动。假设阀芯运动过程为20~15mm(开度变小)和5~10mm(开度变大),进出口压差分别为0.1、0.5、1.0、2.0MPa,初始相对位移为-0.1mm,初始速度和加速度均为0,不同工况下初始流体力不同,并考虑定位器作用,得出介质流向不同时单座阀阀芯的位移与阀芯受到的流体力随时间变化历程,如图10、11所示。
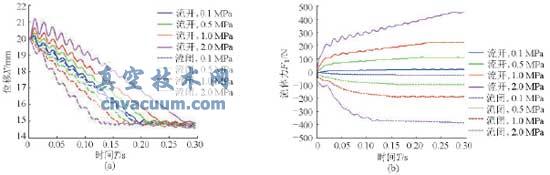
图10 开度为20~15mm时在不同压差下的阀芯振动位移和流体力
(a)位移响应(b)流体力响应
由图10、11可以看出:
(1)阀芯位移从初始位置以振荡衰减的方式到达目标位置,并在目标位置附近作自由振动。
(2)阀芯在向下运动减小开度过程(20~15mm)中,采用流闭流向比采用流开流向,阀芯到达目标位置所用时间更短;当介质为流闭流向时,压差越大,阀芯达到目标位置所用时间越短,而介质为流开流向时,压差越大,阀芯达到目标位置所用时间越长。
(3)阀芯在向上运动增大开度过程(5~10mm)中,采用流开流向比采用流闭流向,阀芯到达目标位置所用时间更短;当介质为流开流向时,压差越大,阀芯到达目标位置所用时间越短,而介质为流闭流向时,压差越大,阀芯达到目标位置所用时间越长。
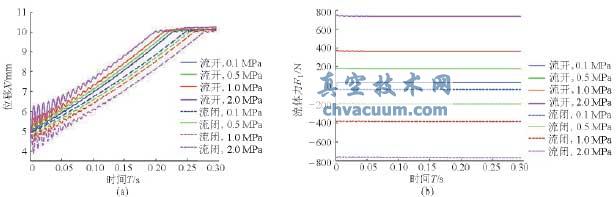
图11 开度为5~10mm时在不同压差下的阀芯振动位移和流体力
(a)位移响应(b)流体力响应
(4)阀芯在向下运动(开度减小)过程中,阀芯受到的流体力从初始位置以振荡衰减的方式到达平衡位置,并在平衡位置附近振动,且到达平衡位置所用时间与位移到达目标位置所用时间相同;介质为流开流向时,压差越大,阀芯受到的流体力达到平衡位置所用时间越长;介质为流闭流向时,压差越大,阀芯受到的流体力达到平衡位置所用时间越短;总体上看,在同一压差下,阀芯在流开流向时受到的流体力要比流闭流向时受到的流体力大。
(5)调节阀在向上运动(开度增大)过程中,阀芯受到的流体力始终处于平衡位置附近,并且在同一压差下,阀芯在流闭流向时受到的流体力比流开流向时受到的流体力大。
4、结论
(1)建立了一个考虑定位器作用的调节阀阀芯-阀杆系统流固耦合动力学模型,并利用ANSYS软件对固定开度和变开度情况、流体流向为流开和流闭情况进行了动态响应仿真分析。
(2)研究结果表明,阀门定位器具有减小阀芯位移振动响应和阀芯位移偏移量的作用,选择合适的定位器参数可以保证调节阀动态性能处于良好状态。对于固定开度情况,无论流闭型还是流开型流向,阀芯稳态位移偏移量以及流体力随压差增加和目标位移减小(开度减小)而增大,阀芯动态位移过渡时间随压差增加而缩短,而流开型流向时阀芯位移响应幅度要大于流闭型流向。对于开度减小情况,采用流闭流向相对流开流向时阀芯动态位移过渡时间更短,采用流闭流向时,压差越大,阀芯动态位移过渡时间越短,而流开流向时则相反;对于开度增大情况,阀芯动态位移过渡时间和压差之间的关系与开度减小情况相反。