差动式快开阀开阀过程动力学分析与仿真
以电磁阀为先导阀,自力式差压控制的快开阀用于模拟产生管线发生破裂时的瞬间泄露工况,在设计时间内快速、稳定的开启是该阀研制的关键技术难点。分析了差动式快开阀的机构及开启原理,以流体力学基本理论为基础,建立了压降随开度变化的关系,完成了阀门开启过程动力学分析与仿真计算,得到了不同阀门开度下的开启时间、速度及加速度,阀芯运动过程中的驱动力逐渐减小,开启时间、开启速度及加速度三者随开度的变化呈非线性变化关系。计算结果表明,阀体开阀时间与实验实测数据吻合良好,开阀过程的速度及加速度与实验结果一致,为工程设计中主要部件的优化研究提供了理论依据。
泄漏是管线常见的事故工况,管线泄漏不仅造成油料的损失,影响管线的正常输送,甚至会导致管线输送中断,直接影响战争后勤油料保障;大量的油料泄漏还会造成严重的环境污染,危及人民的生命财产安全。因此,必须对管线使用和管理人员进行泄漏事故工况的针对性训练,提高处置泄漏事故的能力。
为此,可设计研制一套训练辅助装置,模拟产生瞬间泄漏等事故工况。该装置突发泄漏工况的模拟关键在于快开阀的研制。目前国内外高速开关电磁阀控制流量较小,单一依托电磁阀无法满足该训练辅助装置控制需求。本文研究的快开阀采用电磁控制先导阀,主阀利用差压控制原理,既可有效提高控制流量,其开启响应时间也能满足控制需求。由于该阀在输油现场使用,不宜采用电气原理,而应采用科学、稳定、可靠的液体与机械控制技术来实现高速开启,其中阀体的开阀过程是研制该阀的关键性技术。本文重点介绍了差动式快开阀开阀过程的动力学原理、阀体结构和仿真计算,并对计算结果进行了分析和讨论。
1、阀体结构与开阀过程动力学分析
阀体结构如图1所示。快开阀未动作时,电磁先导阀关闭,流体经孔1流入并充满阀芯内部空腔,流体对阀芯底部压力等于阀芯内部流体压力,弹簧预压力等于底座对阀芯的支持力,阀芯受力平衡。当电磁先导阀通电开启,流体经孔2流出。由于孔2直径远大于孔1直径,流体在阀芯内部无法聚压,阀芯底部受力大于腔内流体压力、弹簧力与流体粘性摩擦力的合力,使阀芯向上运动,阀门开启,大部分流体从阀芯右侧流出。阀门的开启程度由限开度机构控制。
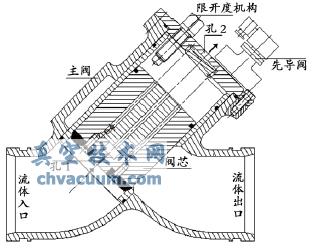
图1 快开阀结构简图

图2 阀内空腔划分图
2、阀体开阀时间计算
如图2所示,阀内空腔直径不同,为了便于分析,将阀内空腔(有流体流经的部分)分为a,1,2,3,4,5几个部分,流体在每个部分流动都相当于在圆管内流动,只是长度和直径有所区别。a部分流量、上下压差、长度、直径分别表示为Qa,ΔPa,La,da;1部分可表示为Q1,ΔP1,L1,d1,其他依次类推。
阀门在开启过程中,空腔内的流体经孔2排出,腔3内流体排出时间即为阀门开启时间。
2.1、阀芯内腔流量计算
主阀阀体是倾斜的,阀芯空腔内划分的各个部分可看成为非水平管。非水平管道层流时,流体重力只影响位能,不影响流动特性。因此,在只讨论速度分布的情况下,阀芯空腔内各个部分流体速度分布可按水平管处理,根据水平管的N-S方程,经进一步计算,水平管内过该截面的流量可表示为:
式中,d为水平管的直径。
2.2、阀芯空腔各部分压差计算
根据圆管流量式(1)得到阀空腔内6个部分的流量,分别为:
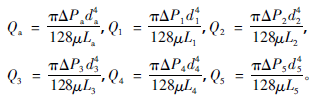
在阀芯向上运动的过程中,a,1,2部分的流体液面不会发生变化,认为流量没有变化,即Qa=Q1=Q2。根据流量关系得:
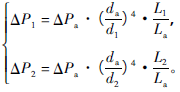 (2)
(2)阀芯向上运动过程中,腔3内流体经孔2中排出,腔3内液位会有明显变化;腔4,5内液位不会产生变化,直到阀门达到最大开度。若dt时间内,阀芯沿轴线方向上升dx,即腔3内有dx长度的流体流出,考虑到从腔2内进入的流量,可表示为:
由于腔4,5内的净剩流量没有变化,则,Q3=Q4=Q5,由6个部分流量表达式及式(3),可以得到下面关系式:

2.3、阀芯腔内壁面粘性摩擦力计算
阀门在开启过程中,流体受挤压经孔2中排出,阀芯内腔壁面会对流体产生一个阻碍其运动的力,这个力就是流体对阀芯内腔内壁面产生的粘性摩擦力。
根据牛顿内摩擦定律,可得管中流体产生的切应力为:
在管壁处τ=τ0,r=R=d/2,则有
于是流体对管壁的摩擦力可表示为:
根据式(4)可以得到,流体对阀空腔内6个部分的摩擦力为:
2.4、压差力计算
为便于计算压差产生的力,将阀芯内腔部分由轴线方向向两侧划
几个区域,区域划分以此前划分的6个部分的直径大小(da 经计算,各部分压差力分别为:
 (6)
(6)
图3 计算压差力时阀内空腔划分图
2.5、阀门开启时间分析
阀门在开启过程中,弹簧受力压缩,弹簧压力f的大小可近似认为等于流体压差力与流体对阀芯内壁面粘性摩擦力的合力,表示为:
将式(5)、(6)代入式(7),得:
将式(2)代入式(8),进一步化简,得:
(9) 式中:
弹簧产生的压力f可表示为:
式中:k表示弹簧的弹性系数;x表示主阀开度,即阀芯沿轴线上升的距离;
表示弹簧的预压量。将上式代入式(9),得:
阀门在开启过程中,a部分流速很大,压差ΔPa比其他几个部分的压差大得多,可近似认为a部分的压差ΔPa同阀芯上下压差ΔP(阀内6个部分压差之和)相等,故式(10)又可表示为:
阀芯向上运动过程中,阀芯上、下的压力差ΔP与主阀开度相关,可表示为ΔP=f(x),其中,x为主阀开度,函数关系f需通过实验测得。则式(11)可变化为:
对式(13)积分,得:
当x=0时,t=0,则
上式可进一步简化,得阀门开启时间为:
本文所研究的阀门跟截止阀原理相同,根据研究,阀门开启时压降与主阀开度之间的关系ΔP=f(x)满足双曲线变化关系,可设:
式中:P0为阀门开启前主阀底部压力,近似为管线运行压力;A,B,C是阀门压降与开度变化关系的系数,可通过实验测得。
阀芯上、下的压降随开度变化关系可经实验测得。在式(14)中代入不同的开度x值,可得不同开度情况下的阀门开启时间。
2.6、分析结果
简化阀门结构,并进行一定的假设,采用数值模拟的方法得到式(15)的系数值;式(14)中,除阀门开度x值外,其余都是已知数,代入不同的主阀开度x值,就可得到不同开度情况下的阀门开启时间理论值。样机实验中,利用瞬变数据采集系统,通过位移传感器,阀芯向上每运动2mm记录一次时间数据,得到不同开度下阀门开启时间实验值。结果见表1。
表1 阀门开启时间理论值、实验值对比

为了直观地反映理论值与实验值之间的关系,将部分数据拟合成曲线,见图4。可以看出,阀门开启时间随开度的变化近似呈线性变化,理论值与实验值吻合良好。
3、仿真计算分析
3.1、开启速度分析
阀门的开启速度即为腔3内液柱长度沿轴线方向的减小速度。根据式(12)得,阀门开启速度为:
式(16)中代入不同的阀门开度x值,即为不同开度时的阀门瞬时速度。
3.2、开启加速度分析
阀门开启加速度是阀门开启速度对时间的倒数,即加速度
将阀门开启速度关系式(16)对时间求导,得:
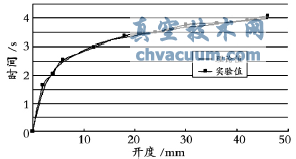
图4 阀门开启时间理论值与实验值对比曲线
式(17)中代入不同的阀门开度x值,即为不同开度时的阀门瞬时加速度。
3.3、分析结果
将上述理论值与实验值进行对比,结果见表2,3。为了直观地反映理论值与实验值之间的关系,将部分数据拟合成曲线,见图5,6。由图5,6可以看出,阀门开启过程的速度随开度的变化逐渐增大,开度越大,速度变化越平稳;加速度随开度的变化逐渐减小。理论值与实验值吻合较好。
表2 阀门开启瞬时速度理论值、实验值对比

表3 阀门开启瞬时加速度理论值、实验值对比

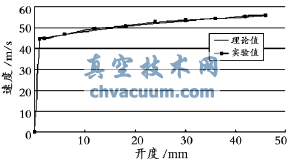
图5 阀门开启瞬时速度理论值与实验值对比曲线
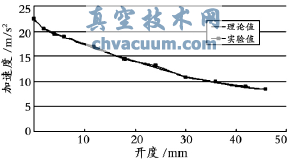
图6 阀门开启瞬时加速度理论值与实验值对比曲线
由速度和加速度变化规律分析可得,阀门开启过程阀芯运动稳定,未受到较大冲击,达到设计要求,满足工程学应用需求。
4、结论
1)利用N-S方程解决了阀门开启过程中液体流速的精确解问题,从而求出了阀芯在不同开度下的开启时间;
2)给出了开阀过程的仿真计算原理、模型、过程和计算结果;
3)计算结果表明,阀门开启到不同开度时,阀芯开启时间与实验实测数据吻合良好,开启过程的速度及加速度与实验结果一致。