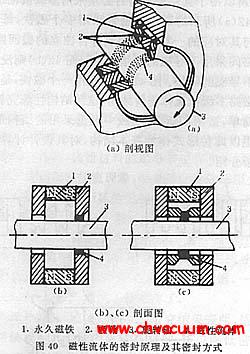
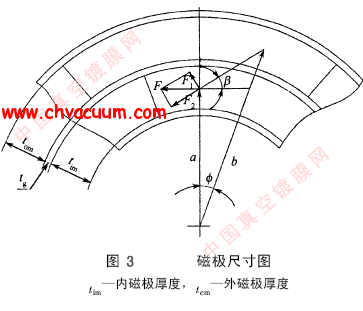
磁性液体密封结构的优化设计(2)

3、算例及结果分析

3.1、优化控制参数及密封结构其它参数的选取

　　算例中选取群体中的个体数M=40 ,非受支配解集合中的个体数N=4 ,最大遗传代数为40,二进制编码位数为20,初始权重系数w1=0.5 , w2=0.5 ,试验步长α= 0.01。密封结构齿数为n=4 ,轴承外径为50mm, 永磁铁材料选为钕铁硼NdFeB-33SH,极靴材料选择电工纯铁DT4,轴材料为45钢。要求的耐压指标对应的各齿下的磁化强度差的和的极大值为Hc = 2.00 ×10⁶A·m^-1 。

3.2、计算结果分析

　　图2 为迭代次数与各目标函数值的关系曲线图。由图中可以看出各目标函数的收敛情况。从第9 代开始,体积目标函数和长度目标函数值分别在两个值之间振荡,当体积函数取较大值时,长度函数取得较小值,但它们的权重和函数值不变。在振荡8 次后,体积函数稳定于较小值,长度函数稳定于较大值。此后又经过5 代的进化,两目标函数分别收敛于某一中间值,一直到进化结束。之所以出现这种收敛过程,一方面是因为使目标权重和函数达到最优的自变量组合并非只有一个,另一方面则是由于权重系数的随机变化。

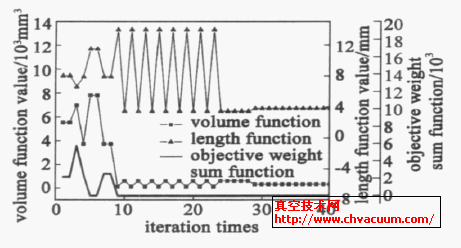
图2 　遗传算法迭代次数与目标函数的关系

　　在迭代40 次后,目标权重和函数最终稳定收敛于5.60 处,而体积函数和长度函数最终分别收敛于325.99mm³ 和3.58mm。表1 列出了初始值、结果参数值及目标函数值。从表中可以看出,优化后磁铁的体积减小了约84.6 % , 极靴长度减小了约57.7 %。

表1 　初始值、结果参数值及目标函数值

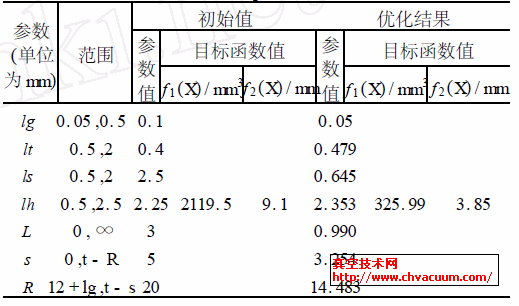
　　图3 为优化前后密封间隙内磁场强度的对比。从中可以明显地看到极靴轴向长度的缩短情况,而且优化后各齿下的磁场强度的最大值比优化前稍高,这样优化后的耐压值也比优化前高,所以优化结果是满足耐压条件的。

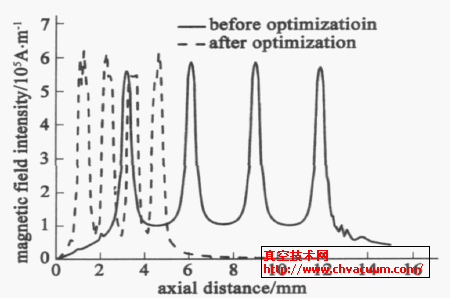
图3 　优化前后密封间隙内磁场强度的对比

　　对比优化前后的参数值及结果值我们发现,在优化后的结构参数下,满足相同耐压值所需的磁铁体积较优化前要小得多。由于密封间隙内磁场强度的大小取决于整个结构的磁路设计,优化结果表明,优化后的结构参数组合可以使磁铁的工作点更加接近于其最大磁能积处。

　　图4 为优化前后密封结构和漏磁情况的对比。其中漏磁曲线表示密封结构横向对称轴上总的磁场强度的变化,其零点从极靴外缘的横向坐标算起,优化前后极靴的外径不变。从图中可以明显看出,优化后密封结构的漏磁比优化前明显减弱。如果用横向对称轴上离极靴外缘5mm 处的磁场强度来衡量漏磁强弱,优化前该处的磁场强度为3.84 ×10⁴A·m^{- 1} , 优化后为0.59 ×10⁴A ·m^{- 1} , 则漏磁减少84.5 %。

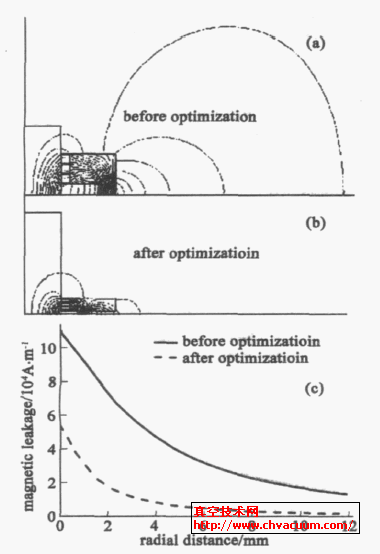
图4 　优化前后密封结构及漏磁情况的对比

　　在实际的密封结构设计中,还要考虑到加工、密封结构的运行条件等各种因素的影响。所以在采用本文的优化方法时,还需根据实际情况,适当限制某些优化参数的范围。比如根据工件运行时轴的径向跳动量来限制间隙的尺寸,根据磁铁的可加工性来限制磁铁的尺寸等。

4、结论

　　多目标混合遗传算法实现的Matlab 编程与Ansys 软件进行交互运算,可以对密封结构进行优化设计。优化后的结构保证了密封耐压,使得磁铁的体积减小了84.6 % ,极靴长度减小了57.7 % ,漏磁减小84.5 % ,这对密封装置的小体积、低成本、低漏磁设计具有重要意义。