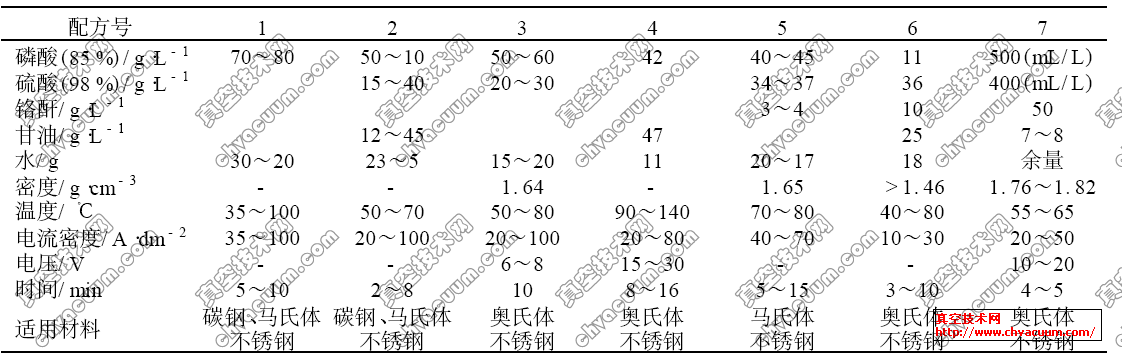
CH与聚变材料Be相互作用的分子动力学模拟

　　采用分子动力学方法模拟了不同能量的CH 粒子与聚变材料Be 的相互作用。根据托卡马克中的环境，入射粒子CH 的模拟入射能量分别设定为低能量( 1，5， 10， 25 eV) 和高能量(50， 100， 150， 200 eV) ，其中碳的沉积率随能量的增大逐渐增加，而氢的沉积率恰好相反。当CH 粒子的入射能量为低能量时，Be 样品表面形成一层碳氢膜; 且其膜厚度越来越薄，并且形成一个厚度逐渐增加中间层; 当入射能量为高能量时，样品中的Be 原子溅射越来越大，入射粒子在样品中的入射深度越来越深，对样品的破坏越来越大，且会在样品中形成一个C 反应层。

　　由于碳基材料具有良好导热性、强抗热冲击性及低原子系数等优点，在ITER 装置选作为偏滤器部件垂直靶中下部和收集板候选材料。在聚变装置运行情况下，从芯部等离子体中逃逸出来的H、D 或T 等载能粒子作用于碳基材料后，将导致碳基材料中的C 原子发生刻蚀现象。刻蚀产物碳氢化合物( CxHy) 在芯部等离子体可能获得更高的能量作用于第一壁材料铍。

　　本文研究的是CH 与Be 样品的相互作用。近年来，各国研究人员在等离子体与壁材料相互作用方面做了大量的研究。Balaji 等通过Ab initio 理论计算研究了Be 与C2H2、C2H4的相互作用。计算结果表明当研究C2H2、C2H4分子与处于基态下或者电子激发状态下的Be 原子相互作用时，有必要考虑分子的扭曲及变形生成的BeC2H2、BeC2H4化合物具是具有高度扭曲变形的基态1A1; 在Be 原子与碳氢化合物相互作用的距离内，基态1A1的最低势能面可避免电子排布的杂化和伴随物的交换，。Ohya 等用分子动力学和蒙特卡洛模拟了等离子体与材料的相互作用。他们的方法是在W 基底上镀上一层碳薄膜，然后用H 轰击C 薄膜层，最后用Be 原子与C、H 混合层相互作用。模拟结果表明当H/( C + H) < 0. 1 时，溅射产物以CH 为主; 随着H/( C + H) 比例的增加，溅射产物逐渐以CH2、CH3为主，Be 原子的注入可以减小大分子的溅射。但是很少人研究CH 与Be 相互作用过程中对入射离子沉积、溅射的微观机理以及入射离子在样品中分布。

　　本文采用分子动力学方法模拟了CH 粒子与Be 表面的相互作用过程，模拟中采用的势函数为Bjorkas 等就发展了Be-C-H 体系Tersoff 势函数，此势函数可以描述原子间相互作用时化学键的断裂和形成。主要研究碳、氢原子的沉积、溅射、对晶格Be 的刻蚀及在样品中的分布来揭示其微观相互作用机制，此研究有利于更全面掌握粒子与壁材料的相互作用，为较少壁损伤提供一定的理论基础。

Be-C-H 体系的势能函数

　　本论文采用Bjorkas 等发展的ABOP( Analytical bondorder potentials) 势能函数来描述Be-C-H系统中粒子之间的相互作用。该势能函数把系统总能量表示为

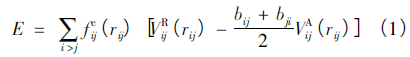
　　式中，E 为系统总能量，r ij表示原子i 和j 之间的距离，fcij( rij) 为截断函数，bij是一个多体的经验键序函数，VR( r) 和VA( r) 分别为原子之间的排斥能和吸引能。式( 1) 中的截断函数fcij( rij) 规定了原子间相互作用的范围，它的形式为

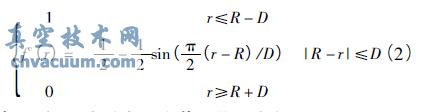
　　式中，R 和D 分别表示为截断范围和间距。

结论

　　本文主要叙述了利用分子动力学方法研究入射能量在1 ～ 200 eV 范围内CH 与Be 样品的相互作用，入射能量对CH 粒子与Be 样品作用的影响显著。低能时，CH 粒子与Be 相互作用主要为沉积行为，在Be 样品表面形成CH 薄膜。而高能时，CH 粒子则会导致样品Be 原子的溅射，形成Be /C /H 的反应层。对薄膜和反应层的性质做了详细的分析，进一步探讨了CH 粒子与Be 样品的相互作用机制C 的溅射。而由高能CH + 在Be 表面形成的反应层中也没有发现大量H 的滞留，在表面也发现了富C层，并有大量的Be-C 键。因此可推断，反应层中有大量的Be /C 化合物，而且十分稳定。这与Guseva等的实验研究是一致的。