螺杆空压机转子受力有限元计算研究

　　螺杆压缩机转子受力的准确计算是保障压缩机可靠性的基本条件。本文利用有限元方法对螺杆空压机阴阳转子所受气体力进行了分析计算，提出了实现转子受力计算的有效、快速的方法及实施方案。同时对转子所受轴向力进行了试验测试，验证了该方法的准确性。

1、前言

　　螺杆压缩机系高速旋转机械，在其运转过程中，由于两转子齿槽的相互挤压，造成齿槽空间的减少，齿槽内的气体压力得到提升，因此造成了转子受力负荷的增加。而螺杆压缩机转子所受气体力的计算为转子的强度、刚度计算，轴承的选择，平衡活塞的设计提供了必要的基础，对研究压缩机的可靠性非常重要。

　　1990 年，Zhou 等利用简化转子复杂表面结构的方法对螺杆转子的受力进行了计算。G. P.Adams 等对螺杆转子进行三维网格划分，并通过积分的方式进行了数值计算，该方法提高了螺杆转子受力计算的精度。邢子文利用转子表面二维网格划分的方法对螺杆转子的受力计算进行了研究，并提出了螺杆压缩机转子受力计算的经典理论和方法。俞论等也利用该方法对螺杆压缩机的转子的受力进行了计算。但由于螺杆转子齿面形状复杂，因此用解析方法计算转子齿面上的气体力对研究人员有较高的要求，推广应用有一定的难度。而采用有限元方法及计算软件进行计算分析，把实际结构模型化，就能使得螺杆转子受力计算的由复杂化变的简单化，同时可以得到更高精度的数值解。

　　本文从双螺杆压缩机转子螺旋曲面的参数方程及转子结构参数出发，利用Ansys 软件对转子的受力进行了有限元方法分析和计算，并进行了试验验证。

2、转子受力有限元计算

　　为了能准确反映螺杆转子受力及其变型的真实性，因此把整个转子( 包括转子齿槽以及轴肩)作为研究对象，建立起转子的三维实体模型，如图1 所示。为了提高转子受力计算的精度，对接触线不再简化，如简化为一条直线，而是对螺杆转子齿槽内的接触线进行了如实的反应，并利用Ansys软件中的波尔运算对转子齿槽中的高、低压工作腔进行了区域划分，如图2 所示。接触线也就成了载荷分布的分界线，因此接触线在齿槽中的分布对整个计算的准确性是至关重要的。然后对整个转子实体进行三维网格的划分，建立其有限元计算模型。

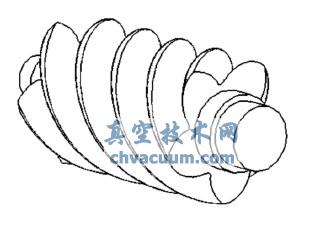
图1 转子实体模型

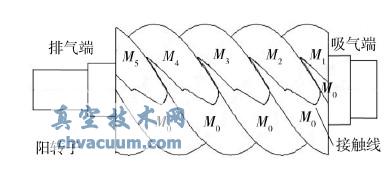
图2 转子接触线及载荷分布

　　2.1、载荷分布确定

　　作用于转子表面上的气体压力在Ansys 软件中是压强与面积的乘积，而压强是一种均布载荷。这种均布载荷在转子表面的分布处理比较简单，只要依靠接触线分割出来的高、低压区域分别予以加载即可。图2 显示了转子齿槽中高、低压的分布区域，图中M1 ～ M5为高压域，M0为低压域。由压缩机工作过程模拟或者通过实验实测得到转子工作腔内压力与阳转子转角关系p = f( θ) ，就可以进行加载。低压域载荷一般处理为吸气压力，即pMo = ps; 而高压域则需要工作腔与阳转子转角关系分别予以赋值。由于图2 中，阳转子齿数为5，假定M1腔内压力为pM1 = f( θ )m，则M2腔内压力为pM2 = f( θm + 72) 、M3腔内压力为pM3= f( θm + 144) 、M4腔内压力为pM4 =f( θm + 216) 、M5腔内压力为pM5 = f( θm + 288) 。对于阴转子，其载荷分布只要与阳转子一样，一一对应即可。

　　2.2、边界条件确定

　　无论计算一个零件的整体或局部，还是计算一个组合机构时，都要考虑其它机构的作用，或者说都要处理边界条件。边界上的位移( 或力) 一般都是未知的，为了简化计算，常常对这些支承条件做一些假设。边界上支承条件简化是否恰当，对结构有限元的计算结构影响较大。另一方面，在形成有限元计算格式时，需要引入已知的位移约束条件，这是为了生成正定的结构刚度距阵。在螺杆压缩机的设计中，无论采用何种形式的结构，都应确保转子的一端固定，另一端能够自由伸缩。一般情况下，转子在排气端轴向定位，在吸气端留有较大的轴向间隙，让其自由膨胀，以便保持排气端有不变的最小间隙值，使排气端面流体泄漏最小，并避免端面磨损。因此在排气端转子轴，轴承对轴的约束作用可以化简为: 圆柱坐标径向方向R 为零位移; 由于排气端轴向定位，限制转子沿Z 轴方向移动的自由度，仅保证转子绕Z 轴旋转一个切向θ 自由度。在吸气端，轴承对转子的约束作用可以化简为: 圆柱坐标径向方向R 为零位移，保留转子绕Z 轴旋转的切向θ 自由度和沿Z 方向自由度。

　　通过以上设置，就可以对螺杆压缩机中的转子受力进行有限元计算( 适用于任何工质) ，可通过软件后处理程序得到转子轴向受力、排气端径向受力、吸气端径向受力等。

5、结论

　　( 1) 利用有限元方法可以非常方便地计算出螺杆压缩机的转子受力情况，大大降低了计算的难度，而且精度较高，完全能满足工程应用的需要;

　　( 2) 在螺杆压缩机中，力值最大分别为阳转子轴向力、阴转子排气端径向力和阳转子排气端径向力，而承担这3 个力的轴承都在排气端，因此排气端的轴承选择是保障螺杆压缩机可靠性的基础。