检漏容器的密封性能对航天器总漏率测试的影响研究

　　采用非真空氦质谱累积法进行航天器密封系统的总漏率测试时，需要检漏容器对密封系统泄漏出的氦气进行收集。本文通过理论分析，并用正压氦漏孔模拟航天器密封系统的泄漏进行试验验证，得出了检漏容器的密封性能对航天器密封系统总漏率测试的影响，为检漏容器的泄漏给出了建议指标。

　　采用非真空氦质谱累积法进行航天器密封系统总漏率测试时，需要检漏容器在大气环境下对泄漏出的氦气进行收集，以便通过一定时间内氦气在检漏容器内的浓度变化得到系统总漏率，因此检漏容器的密封性能是总漏率测试的重要影响因素之一。

　　最理想的情况是检漏容器完全不漏，密封系统泄漏出的氦气被全部收集和检测，可最大限度地保证测试的准确度。但完全不漏的密封容器是不存在的，同时过高的漏率指标会大大增加检漏容器的制造和维护成本。目前国内航天器进行非真空氦质谱累积法检漏时，一般要求密封容器泄漏指标为密封容器内充气2 kPa，24 h 后压降值不大于200 Pa。

　　本研究利用正压漏孔和小型密封容器模拟航天器密封系统在检漏容器中的泄漏，通过理论分析和试验验证，得到检漏容器的密封性能对航天器总漏率测试的影响，提出检漏容器的漏率指标和建议。

1、理论分析

　　1.1、压力关系分析

　　在航天器密封系统进行总漏率测试的初始时刻，检漏容器内压力P1 等于当地大气环境压力P0。在测试周期内，因环境温度变化、检漏容器泄漏等的影响，P1 与P0 的关系可以分为以下几种：

　　a)P1 一直不高于P0，即P1≤P0；

　　b)P1 一直不低于P0，即P1≥P0；

　　c)P1 与P0 关系不确定，即P1≤P0 与P1≥P0 交替出现。

　　以下针对上述3 种关系，对检漏容器泄漏造成的总漏率测试影响进行分析。

　　1.2、泄漏影响分析

　　1.2.1、P1 不高于P0 的情况下

　　大气中的氦浓度约为5 ppm，记为γ0，航天器泄漏引起的检漏容器内氦浓度的增量记为γ1，一般不超过0.5 ppm，由此引起的检漏容器内压力的增量与P0 相比可忽略不计。

　　假设航天器密封系统总漏率测试过程中，检漏容器内压力一直不高于当地大气压，即P1≤P0，则检漏容器外的环境大气可通过检漏容器上存在的漏孔进入检漏容器内部，使检漏容器内部压力增高。假设气体由检漏容器外至容器内的扩散为等比扩散，则检漏容器内部压力增加ΔP 后的氦浓度γΔP 的估算见公式(1)。

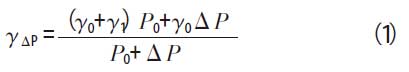
　　若航天器密封系统总漏率测试周期24 h 内，允许检漏容器因泄漏造成的总漏率测试相对误差不大于5%，则可得γΔP 与γ0、γ1 的关系见公式(2)。

　　将公式(1)代入公式(2)，经计算可得允许的压力增加值ΔP≤5 332 Pa，由此可知：在航天器密封系统总漏率测试过程中，满足P0-P1≤5 332 Pa的条件下，由检漏容器泄漏造成的测量相对误差不大于5%。

　　1.2.2、P1 不低于P0 的情况下

　　假设航天器密封系统总漏率测试过程中，检漏容器内压力一直不低于当地大气压，即P1≥P0，则检漏容器内的气体可通过检漏容器上存在的漏孔扩散至环境大气中，使检漏容器内的压力下降。因航天器泄漏引起的检漏容器内压力的增量与P0相比可忽略不计、容器内氦浓度的变化量远小于环境大气的氦浓度γ0，假设气体由检漏容器内至容器外的扩散为等比扩散，则检漏容器因泄漏导致内部压力降低ΔP 后的氦浓度γΔP 的估算见公式(3)。

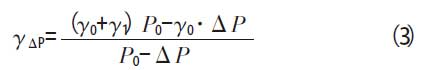
　　若航天器密封系统总漏率测试周期24 h 内，允许检漏容器因泄漏造成的总漏率测试相对误差不大于5%，则将公式(3)代入公式(2)，经计算可得允许的压降值ΔP≤4 825 Pa，由此可知：在航天器密封系统总漏率测试过程中，满足P0-P1≤4 825 Pa的条件下，由检漏容器泄漏造成的测量相对误差不大于5%。

　　1.2.3、P1 与P0 不定关系的情况下

　　假设航天器型号产品总漏率测试过程中，检漏容器内压力有时高于环境大气压力，有时低于环境大气压力，即P1≤P0 或P1≥P0 的情况交替出现，因此由检漏容器泄漏造成的氦浓度变化应不大于P1≤P0 和P1≥P0 情况下的最小值。由此可知：在航天器密封系统总漏率测试过程中，满足P0-P1≤4 825 Pa或P1-P0≤4 825 Pa 的条件下，由检漏容器泄漏造成的测量相对误差不大于5%。

2、试验系统及方案

　　2.1、试验系统

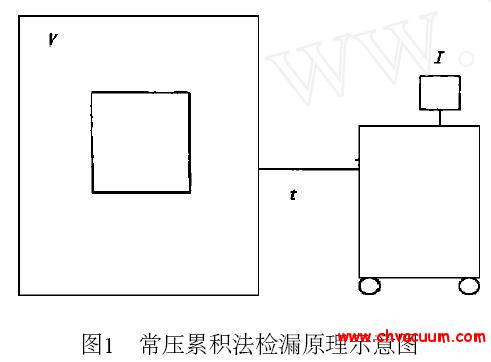
　　为研究检漏容器的泄漏对航天器密封系统总漏率测试的影响，特设计一套试验系统，主要由小型密封容器、标准漏孔、压力计、氦质谱检漏仪和测试计算机等组成。小型密封容器可收集有源漏孔泄漏出的氦气，用于模拟航天器检漏容器；有源漏孔自带气室，可向小型密封容器内持续漏出氦气，用于模拟航天器密封系统在检漏容器内的泄漏；无源漏孔安装在小型密封容器上使小型密封容器获得不同的漏率，用于模拟检漏容器的不同泄漏状态。试验系统原理图见图1，主要仪器设备性能参数见表1。

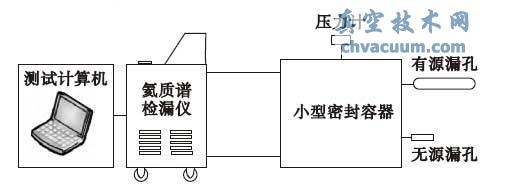
图1 试验系统原理图

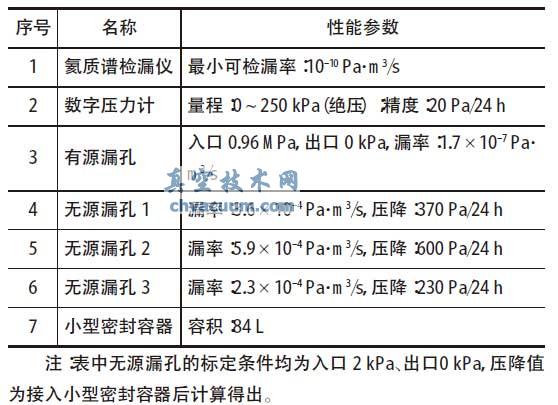
表1 试验系统所用仪器设备

　　2.2、试验方案

　　2.2.1、试验环境

　　将试验系统置于航天器总装大厅内，以获得与航天器密封系统总漏率测试时相同的测试环境，避免因测试环境的差异带来的影响。

　　2.2.2 试验原理

　　按图1 搭建试验系统，在大气环境下密封小型密封容器后，对容器内的氦浓度进行测试并开始计时，在1 个测试周期(24 h)内，对容器内的氦气浓度至少进行5 次测试，测得的数据通过最小二乘法可得到容器内的氦浓度随时间的变化曲线，其表达见公式(4)。

　　将k 称为漏率斜率，则容器内氦气浓度增量Δγ 随时间的变化关系，见公式(5)。

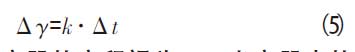
　　将小型密封容器的容积记为V，当容器内的氦分压增量ΔPHe<<P1 时，有源漏孔漏率Q 的计算见公式(6)。

　　由公式(6)可知，当小型密封容器无泄漏时，有源漏孔的真实漏率Q0=k0P1V；当小型密封容器有泄漏时，假设因泄漏造成的容器内压力变化与P1相比可忽略不计，则有源漏孔的测试漏率Qi=kiP1V；因此小型密封容器泄漏造成的有源漏孔漏率的测试相对误差ηi 的计算见公式(7)。

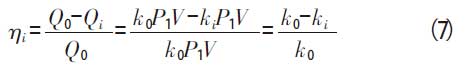
　　因此，通过试验得到有源漏孔在小型密封容器不同泄漏情况下的漏率斜率，经过比较和计算即可得到容器的密封性能对有源漏孔漏率测试的影响。

　　2.2.3、试验步骤

　　首先在总装大厅内，与航天器密封系统总漏率测试相同的环境下进行试验，步骤如下：

　　a)小型密封容器不接无源漏孔，即无泄漏情况下，有源漏孔的标称漏率斜率k0 的测试；

　　b)小型密封容器依次接入不同漏率的无源漏孔，使小型密封容器获得不同的泄漏量Qi，在此情况下进行有源漏孔漏率斜率k0i 的测试。

　　其次，预先向小型密封容器内充入2 kPa 的氮气，使小型密封容器内压力高于环境大气压力，在此极限情况下，进行小型密封容器不同泄漏量Qi时有源漏孔漏率斜率k1i 的测试。

3、试验

　　3.1、密封容器无泄漏时k0 测试

　　试验系统不接无源漏孔，即小型密封容器近似无泄漏，通过试验获得的有源漏孔的氦浓度-时间曲线及标称漏率斜率k0 见图2。图中氦浓度是试验系统中氦质谱检漏仪测得的漏率值，是氦浓度大小的间接反映，与实际氦浓度存在固定的倍数关系。

　　由图2 可得，当小型密封容器无泄漏时，有源漏孔的标称漏率斜率k0=2.436×10^-14。此斜率为基准斜率，当小型密封容器接入不同的无源漏孔后，因泄漏的影响，必然会使测得的斜率值偏离基准斜率。

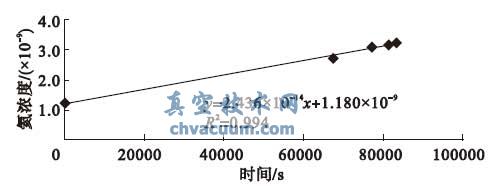
图2 k0 氦浓度- 时间曲线

　　3.2、密封容器有泄漏时k0i 测试

　　3.2.1、密封容器接无源漏孔

　　先后将无源漏孔1、无源漏孔2 接入小型密封容器，通过试验获得的有源漏孔的氦浓度- 时间曲线及漏率斜率k01、k02，分别见图3 和图4。

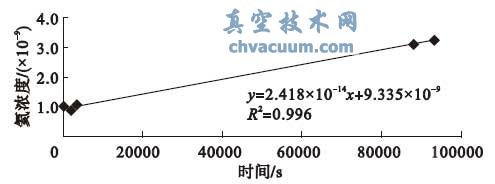
图3 k01 氦浓度- 时间曲线

图4 k02 氦浓度- 时间曲线

　　由表1 可知，小型密封容器接入无源漏孔1，则容器充气2 kPa、保压24 h 后的压降值为370 Pa，为目前检漏容器允许漏率的1.8 倍；小型密封容器接入无源漏孔2，则容器充气2 kPa、保压24 h 后的压降值为600 Pa，为目前检漏容器允许漏率的3倍。由上图可得，有源漏孔的漏率斜率k01=2.418×10^-14，k02=2.404×10^-14， 根据公式7 可得到η01=0.7%，η02=1.3%，即此2 种泄漏情况下，有源漏孔的漏率斜率与标称漏率斜率k0 的相对误差均不大于5%，说明检漏容器的泄漏量为目前允许漏率的3 倍时，由检漏容器的泄漏引起的总漏率测试的相对误差不大于5%。

　　3.2.2、密封容器接准4×40 通孔

　　为验证检漏容器在大泄漏量下对总漏率测试影响不大于5%的结论，在小型密封容器上接入准4×40 的通孔，通过试验获得的有源漏孔的氦浓度- 时间曲线及漏率斜率k03 见图5。

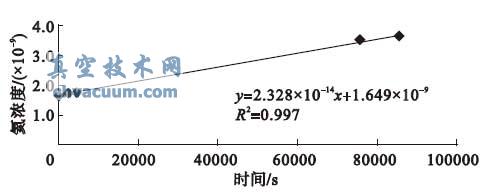
图5 k03 氦浓度- 时间曲线

　　小型密封容器接入准4×40 的通孔后，无法在容器内部建立高于环境大气的压力，即容器的泄漏远大于充气2 kPa、保压24 h 压降为2 kPa的情况。由图5 可知，有源漏孔的漏率斜率k03=2.328×10^-14，根据公式7 可得到η03=4.4%，即此状况下有源漏孔的漏率斜率与标称漏率斜率k0 的相对误差不大于5%，由此说明检漏容器的泄漏量至少为目前允许漏率的10 倍时，由检漏容器的泄漏引起的总漏率测试的相对误差不大于5%。

　　3.3、极限情况下测试

　　分别将无源漏孔3、无源漏孔2 接入小型密封容器，向容器内预充入2 kPa 的氮气后，通过试验获得的有源漏孔的氦浓度- 时间曲线及漏率斜率k11、k12，分别见图6 和图7。

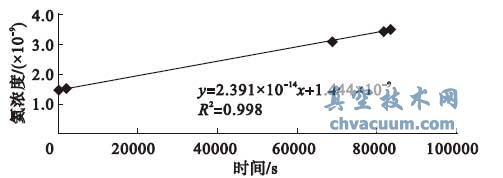
图6 k11 氦浓度- 时间曲线

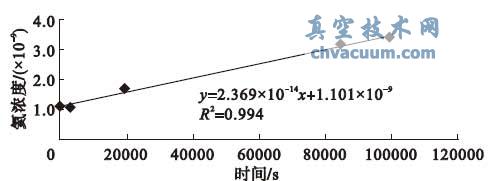
图7 k12 氦浓度- 时间曲线

　　由表1 可知，小型密封容器接入无源漏孔3，则容器充气2 kPa、保压24 h 后的压降值为230 Pa，为目前检漏容器允许漏率的1.1 倍；小型密封容器接入无源漏孔2，则容器充气2 kPa、保压24 h 后的压降值为600 Pa，为目前检漏容器允许漏率的3倍。由上图可得，有源漏孔的漏率斜率k11=2.391×10^-14，k02=2.369×10^-14， 根据公式7 可得到η11=1.8%，η12=2.7%，即此2 种极限情况下，有源漏孔的漏率斜率与标称漏率斜率k0 的相对误差均不大于5%，说明在测试的起始时刻检漏容器内部压力高于环境大气压2 kPa 且检漏容器的泄漏量为目前允许漏率的3 倍时，由检漏容器的泄漏引起的总漏率测试的相对误差不大于5%。此状态为假设的极限状况，在航天器总漏率测试中不可能存在，其测试的相对误差大于相同试验系统下正常条件下测试的相对误差。

4、结论

　　通过分析非真空氦质谱累积法进行航天器密封系统总漏率测试时，检漏容器内气体压力、氦气浓度变化与总漏率测试结果之间的关系，并通过试验验证，得出以下结论：在大气环境下进行航天器密封系统总漏率测试时，若检漏容器漏率满足充压2 kPa、压降不大于2 kPa/24 h 的要求，则密封容器的泄漏对总漏率测试结果的影响不大于5%。对比目前对检漏容器的密封要求，提出以下建议：

　　a)对只具有检漏功能的检漏容器，放宽漏率要求至充压2 kPa、压降不大于2 kPa/24 h；

　　b)对同时具有运输包装箱功能的检漏容器维持现有要求，即充压2 kPa、压降不大于200 Pa/24 h。