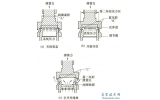
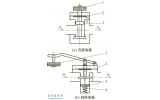
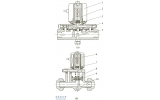
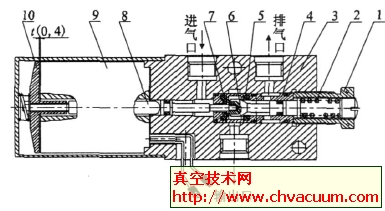
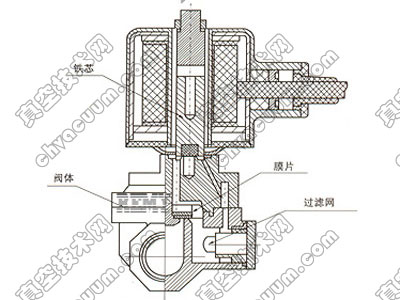
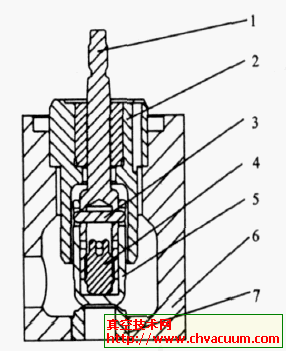
球面密封气动截止阀用气缸力的技术研究(2)

　　由计算结果知道,假定密封面宽度b=3mm 时,满足qMF< q< [q]的要求。实际测量2台已经使用的阀门,其密封面宽度分别为2.4mm与2.6mm,与计算结果接近,证明该计算方法具有一定的科学性。

3.2、弹塑性分析法

　　由于传统设计方法在设计之初对于假定密封面没有依据,只能是随意假定后经过试差取得满意的结果,这样计算试差的次数比较多也比较繁琐。为了实现设计过程的简化和使得密封面的假定更有理论依据少走弯路,笔者进行了研究并通过大量的数学计算,在传统设计方法的基础上进行了假设。既然普遍认为在球形密封结构中的球体在接触应力的作用下发生了弹塑性变形,也正是球体的弹塑性变形实现密封性能。那么阀门空载时在气缸力的作用下(即管道没有介质, 阀门为常闭状态时) , 密封面上的应力就不应该大于材料的屈服极限,如果大于屈服极限,塑性变形势必会继续加大,直到密封面的应力等于或小于屈服极限。以此理论为依据对阀门受力进行分析。首先是根据介质静压力QM J估算气缸直径并圆整,再根据气缸直径计算密封面宽度b,根据密封面宽度b计算必须比压qMF , 确定实际比压q。如果实际比压q不能满足qM F < q <〔q〕的要求,则对气缸重新假设,重复以上计算过程直到满足要求为止。举例, 由传统计算方法知介质静压力QMJ=40109N,F=QMJ ,计算气缸内径D=101mm,取D=115mm 进行试算(试差过程省略) 。

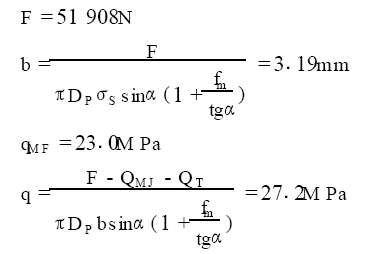
　　计算结果满足qM F < q < [q]的要求, 密封面宽度3.19mm 与实际测量值2.4mm 和2.6mm 的误差分别为25%和18.5%。笔者认为造成该结果的原因应该主要是材料标准中规定H62的屈服强度为最低要求,而实际材料均高于该值要求。以工作压力P = 20M Pa, 密封面直径DP =73.36mm,锥半角α = 30°,气缸内径<=180mm,其他条件相同的气动截止阀为例进行计算(计算过程先忽略所有摩擦力) 。介质静压力QMJ =84492N,F=QMJ, 计算气缸内径D=147mm, 取D=180mm,QT = 6 000N,试差过程省略。则F = 127170N, b=5.16mm, qMF = 32.0MPa, q=45.8MPa, 计算结果满足qM F < q < [q]的要求。

 　　在传统设计方法和弹塑性分析方法中均没有考虑气缸效率,所以相应对阀门加工精度要求较高,并且在气缸与活塞之间涂抹了润滑油, 实际摩擦力很小。现在在设计该类阀门时均引入了气缸效率η,这样使得阀门气缸内径增大, 设计完成以后需要校核不考虑气缸效率时在工作状态密封面的实际比压,使之小于材料的许用比压。

4、结语

　　设计过程中传统设计法直接假定密封面宽度进行气缸设计,而弹塑性分析法以粘着理论为依据认为球体发生了弹塑性变形,也正是球体的弹塑性变形实现了密封性能, 所以弹塑性分析法是实际计算密封面宽度。在实际设计过程中,为了减小误差笔者建议密封材料的屈服强度采用实际测定值, 因为标准中的数值为最低要求,一般与实测值差距均比较大。两种方法均能完成气缸的设计过程, 在实际应用中传统设计方法比弹塑性法广泛, 但笔者认为弹塑性法比传统法更有理论依据,在设计过程中可以少走弯路。