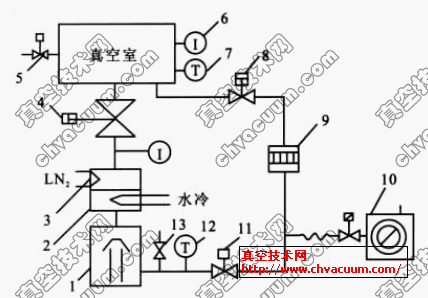
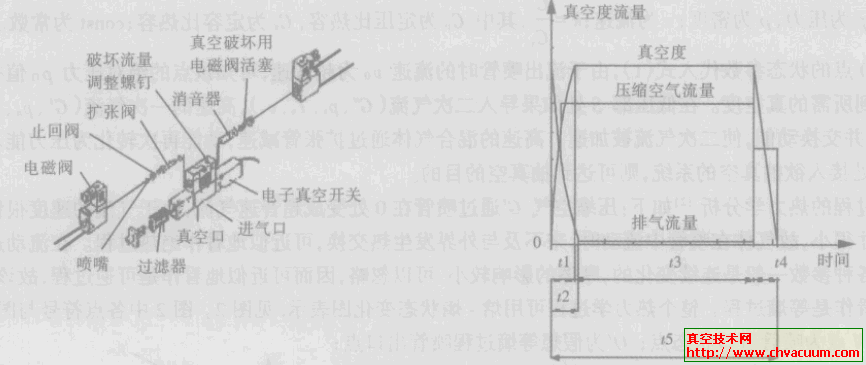
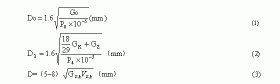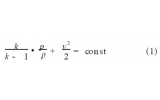真空发生器系统的物理和数学模型(2)
对于上述的真空发生器系统,配管内的流动为一维可压缩、带摩擦、热传导的非定常流动,其支配方程为
连续方程
状态方程p =ρRT(4)
在式(1)~(3)偏微分方程中,密度ρ、流速u 和压力p 是因变量,两个自变量是沿管距离x和时间t。这三个偏微分方程可以用特征线方法变换成全微分方程,即三条特征线上的三组特征相容关系。
带内插的特征线法
用dt乘式(5)~(7),并在积分中采用一阶近似,特征相容方程的有限差分形式为
在C0 特征线上
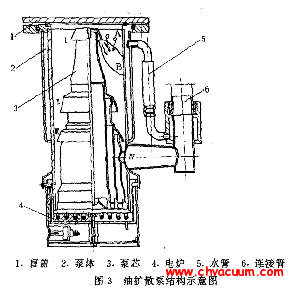
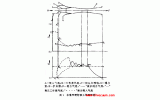
在式(8)~(10) 中, 上标表示时步, 下标表示网格点或内插点,如图3所示。图中t 时刻网格点i-1,i,i+1上的p, u,ρ值由初始条件或上一时步计算得到,内插点i+,i0,i-上的p,u,ρ值由i-1,i,i+1三点值插值得到,对于t +Δt时刻a点的p,u,ρ由三个特征相容关系式求出。
图3 规定时间间隔的带内插的特征线方法示意图
边界条件的确定
由图2 可见,由配管内点可引三条特征线,故有三组特征相容方程求解三个未知数p , u ,ρ。而对于与吸盘相连的进口边界只能引一条特征线, 故只有一组特征相容关系;与真空发生器相连出口边界也只能引两条特征线,故也只有二组特征相容关系,因此均需引入p , u ,ρ的补充关系式,即相应的边界条件,以求解边界上不同时刻的p,u,ρ。
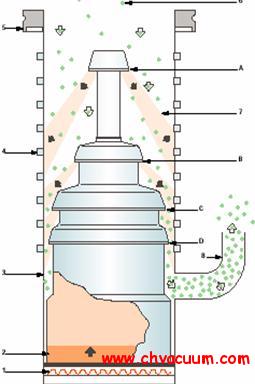
与吸盘相连的进口边界
采用气室模型 ,则有
P/ργ = 常数,ρV = m
式中V为吸盘及其与配管相连的管接头内的体积;m为该体积内的气体质量。
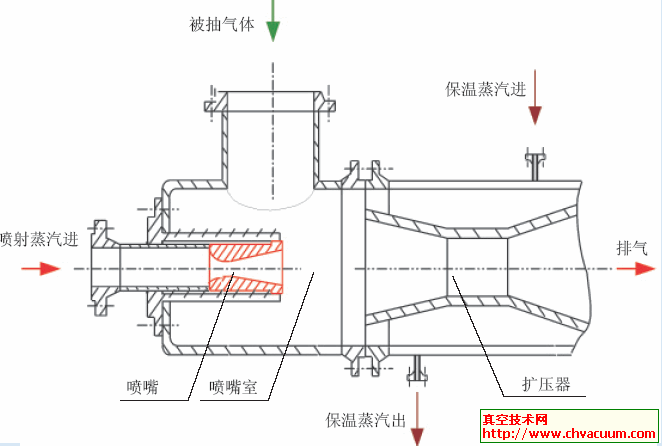
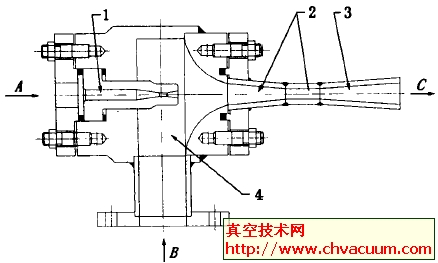
与真空发生器相连的出口边界
根据真空发生器的流量特性, 补充真空压力p和吸入流量(QV=uA)的关系式。由此可见对于与吸盘相连的进口边界补充两组关系式,对与真空发生器相连的出口边界补充一组关系式,即可得到不同时刻进、出口上的p,u,ρ值。
其它相关文章: